HEAD

Chapter 11
Monte Carlo Techniques

So far we have been focussing on how particle codes work once the particles are launched. We've talked about how they are moved, and how self-consistent forces on them are calculated. What we have not addressed is how they are launched in an appropriate way in the first place, and how particles are reinjected into a simulation. We've also not explained how one decides statistically whether a collision has taken place to any particle and how one would then decide what scattering angle the collision corresponds to. All of this must be determined in computational physics and engineering by the use of random numbers and statistical distributions.⁶⁶ Techniques based on random numbers are called by the name of the famous casino at Monte Carlo.

11.1 Probability and Statistics

11.1.1 Probability and Probability Distribution

Probability, in the mathematically precise sense, is an idealization of the repetition of a measurement, or a sample, or some other test. The result in each individual case is supposed to be unpredictable to some extent, but the repeated tests show some average trends that it is the job of probability to represent. So, for example, the single toss of a coin gives an unpredictable result: heads or tails; but the repeated toss of a (fair) coin gives on average equal numbers of heads and tails. Probability theory describes that regularity by saying the probability of heads and tails is equal. Generally the probability of a particular class of outcomes (e.g. heads) is defined as the fraction of the outcomes, in a very large number of tests, that are in the particular class. For a fair coin toss, probability of heads is the fraction of outcomes of a large number of tosses that is heads, 0.5. For a six-sided die, the probability of getting any particular value, say 1, is the fraction of rolls that come up 1, in a very large number of tests. That will be one-sixth for a fair die. In all cases, because probability is defined as a fraction, the sum of probabilities of all possible outcomes must be unity.

More usually, in describing physical systems we deal with a continuous real-valued outcome, such as the speed of a randomly chosen particle. In that case the probability is described by a "probability distribution" p(v) which is a function of the random variable (in this case velocity v). The probability of finding that the velocity lies in the range v→ v+dv for small dv is then equal to p(v)dv. In order for the sum of all possible probabilities to be unity, we require

⌠
⌡

p(v) dv = 1.

(11.1)

Each individual sample ⁶⁷ might give rise to more than one value. For example the velocity of a sampled particle might be a three-dimensional vector v=(v_x,v_y,v_z). In that case, the probability distribution is a function in a multi-dimensional parameter-space, and the probability of obtaining a sample that happens to be in a multi-dimensional element d³v at v is p(v)d³v. The corresponding normalization is

⌠
⌡

p(v) d³v = 1.

(11.2)

Obviously, what this shows is that if our sample consists of randomly selecting particles from a velocity distribution function f(v), then the corresponding probability function is simply

p(v) = f(v)/

⌠
⌡

f(v)d³v = f(v)/n,

(11.3)

where n is the particle density. So the normalized distribution function is the velocity probability distribution.

The cumulative probability function can be considered to represent the probability that a sample value is less than a particular value. So for a single-parameter distribution p(v), the cumulative probability is

P(v) =

⌠
⌡

v

−∞

p(v′)dv′.

(11.4)

In multiple dimensions, the cumulative probability is a multidimensional function that is the integral in all the dimensions of the probability distribution:

P(v) = P(v_x,v_y,v_z)=

⌠
⌡

v_x

−∞

⌠
⌡

v_y

−∞

⌠
⌡

v_z

−∞

p(v′)d³v′.

(11.5)

Correspondingly the probability distribution is the derivative of the cumulative probability: p(v)=dP/dv, or p(v)=∂³P/∂v_x∂v_y∂v_z.

11.1.2 Mean, Variance, Standard Deviation, and Standard Error

If we make a large number N of individual measurements of a random value from a probability distribution p(v), each of which gives a value v_i, i=1,2,...,N, then the sample mean value of the combined sample N is defined as

μ_N =

N
∑
i=1

v_i.

(11.6)

The sample variance is defined⁶⁸ as

S_N² =

N−1

N
∑
i=1

(v_i−μ_N)².

(11.7)

The sample standard deviation is S_N, the square root of the variance, and the sample standard error is S_N/√N. The mean is obviously a measure of the average value, and the variance or standard deviation is a measure of how spread out the random values are. They are the simplest unbiassed estimates of the moments of the distribution. These moments are properties of the probability distribution not of the particular sample. The distribution mean⁶⁹ is defined as

μ =

⌠
⌡

v p(v) dv

(11.8)

and the distribution variance is

S² =

⌠
⌡

(v−μ)² p(v)dv.

(11.9)

Obviously for large N we expect the sample mean to be approximately equal to the distribution mean and the sample variance equal to the distribution variance.

A finite size sample will not have a mean exactly equal to the distribution mean because of statistical fluctuations. If we regard the sample mean μ_N as itself being a random variable, which changes from one total sample of N tests to the next total sample of N tests, then it can be shown⁷⁰ that the probability distribution of μ_N is approximately a Gaussian with standard deviation equal to the standard error S_N/√N. That is one reason why the Gaussian distribution is sometimes called the "Normal" distribution. The Gaussian probability distribution in one dimension has only two⁷¹ independent parameters μ and S.

11.2 Computational random selection

Computers can generate pseudo-random numbers, usually by doing complicated non-linear arithmetic starting from a particular "seed" number (or strictly a seed "state" which might be multiple numbers). Each successive number produced is actually completely determined by the algorithm, but the sequence has the appearance of randomness, in that the values v jump around in the range 0 ≤ v ≤ 1, with no apparent systematic trend to them. If the random number generator is a good generator, then successive values will not have statistically-detectable dependence on the prior values, and the distribution of values in the range will be uniform, representing a probability distribution p(v)=1. Many languages and mathematical systems have library functions that return a random number. Not all such functions are "good" random number generators. (The built-in C functions are notoriously not good.) One should be wary for production work. It is also extremely useful, for example for program debugging, to be able to repeat a pseudo-random calculation, knowing the sequence of "random" numbers you get each time will be the same. What you must be careful about, though, is that if you want to improve the accuracy of a calculation by increasing the number of samples, it is essential that the samples be independent. Obviously, that means the random numbers you use must not be the same ones you already used. In other words, the seed must be different. This goes also for parallel computations. Different parallel processors should normally use different seeds.

Now obviously if our computational task calls for a random number from a uniform distribution between 0 and 1, p(v)=1, then using one of the internal or external library functions is the way to go. However, usually we will be in a situation where the probability distribution we want to draw from is non-uniform, for example a Gaussian distribution, an exponential distribution, or some other function of value. How do we do that?

We use two related random variables; call them u and v. Variable u is going to be uniformly distributed between 0 and 1. (It is called a "uniform deviate".) Variable v is going to be related to u through some one-to-one functional relation. Now if we take a particular sample value drawn from the uniform deviate, u, there is a corresponding value v. What's more, we know that the fraction of drawn values that are in a particular u-element du, is equal to the fraction of values that are in the corresponding v-element dv. Consequently, recognizing that those fractions are p_u(u)du and p_v(v)dv respectively, where p_u and p_v are the respective probability distributions of u and v, we have

p_u(u)du=p_v(v)dv ⇒ p_v(v) = p_u(u)

⎢
⎢

(11.10)

The final equality uses the fact that p_u=1 for a uniform deviate.

Therefore, if we are required to find random values v from a probability distribution p_v, we simply have to find a functional relationship between v and u that satisfies p_v(v) = |du/dv|. But we know of a function already that provides this property. Consider the cumulative probability P_v(v)=∫^vp_v(v′)dv′. It is monotonic, and ranges between zero and 1. Therefore we may choose to write

u = P_v(v) for which

= p_v(v).

(11.11)

So if u=P_v(v), the v variable will be randomly distributed with probability distribution p_v(v). We are done. Actually not quite done, because the process of choosing u and then finding the value of v which corresponds to it requires us to invert the function P_v(v). That is

v = P_v⁻¹(u).

(11.12)

Fig. 11.1 illustrates this process. It is not always possible to invert the function analytically, but it is always possible to do it numerically. One way is by root finding e.g. bisection.

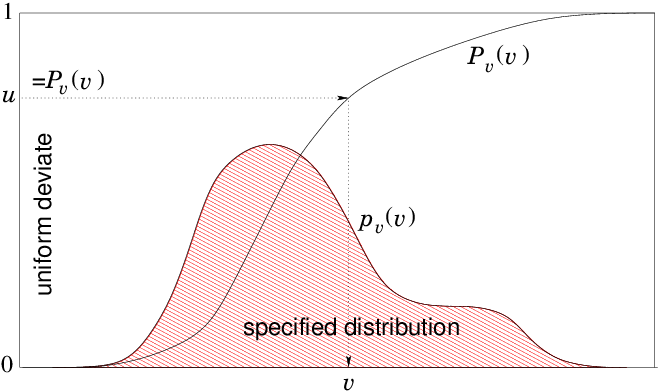
Figure 11.1: To obtain numerically a random variable v with specified probability distribution p_v (not to scale), calculate a table of the function P_v(v) by integration. Draw a random number from uniform deviate u. Find the v for which P_v(v)=u by interpolation. That's the random v.

Since P_v is monotonic, for any u between 0 and 1, there is a single root v of the equation P_v(v)−u=0. Provided we can find that root quickly, then given u we can find v. One way to make the root finding quick is to generate a table of N_t values of v and u=P_v(v), equally spaced in u (not in v). Then given any u, the index of the point just below u is the integer value i= u*N_t, and we can interpolate between it and the next point using the fractional value of u*N_t.⁷²

Rejection Method Another way of obtaining random values from some specified probability distribution is by the "Rejection Method", illustrated in Fig. 11.2. This involves using a second random number to decide whether or not to retain the first one chosen. The second random number is used to weight the probability of the first one.

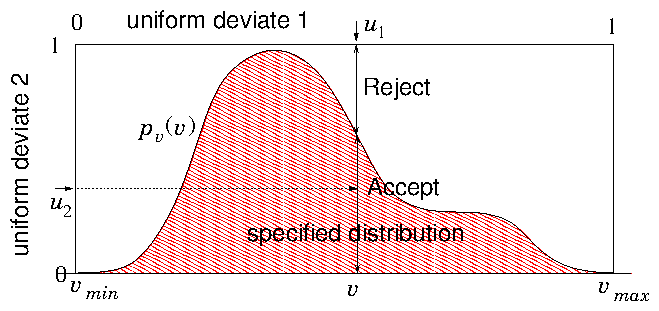
Figure 11.2: The rejection method chooses a v value randomly from a simple distribution (e.g. a constant) whose integral is invertible. Then a second random number decides whether it will be rejected or accepted. The fraction accepted at v is equal to the ratio of p_v(v) to the simple invertible distribution. p_v(v) must be scaled by a constant factor to be everywhere less than the simple distribution (1 here).

In effect this means picking points below the first scaled distribution, in the illustrated case of a rectangular distribution, uniformly distributed within the rectangle, and accepting only those that are below p_v(v) (suitably scaled to be everywhere less than 1). Therefore some inefficiency is inevitable. If the area under p_v(v) is, say, half the total, then twice as many total choices are needed, and each requires two random numbers, giving four times as many random numbers per accepted point. Improvement on the second inefficiency can be obtained by using a simply invertible function that fits p_v(v) more closely. Even so, this will be slower than the tabulated function method, unless the random number generator has very small cost.

Monte Carlo Integration Notice by the way, that this second technique shows exactly how "Monte Carlo Integration" can be done. Select points at random over a line, or a rectangular area in two dimensions, or cuboid volume in three dimensions. Decide whether each point is within the area/volume of interest. If so, add the value of the function to be integrated to the running total, if not, not. Repeat. At the end multiply the total by the area/volume of the rectangle/cuboid divided by the number of random points examined (total, not just those that are within the area/volume). That's the integral. Such a technique can be quite an efficient way, and certainly an easy-to-program way, to integrate over a volume for which it is simple to decide whether you are inside it but hard to define systematically where the boundaries are. An example might be the volume inside a cube but outside a sphere placed off-center inside the cube. The method's drawback is that its accuracy increases only like the inverse square root of the number of points sampled. So if high accuracy is required, other methods may be much more efficient.⁷³

11.3 Flux integration and injection choice.

Suppose we are simulating a sub-volume that is embedded in a larger region. Particles move in and out of the sub-volume. Something interesting is being modelled within the subvolume, for example the interaction of some object with the particles. If the volume is big enough, the region outside the subvolume is relatively unaffected by the physics in the subvolume, then we know or can specify what the distribution function of particles is in the outer region, at the volume's boundaries. Assume that periodic boundary conditions are not appropriate, because, for example, they don't well represent an isolated interaction. How do we determine statistically what particles to inject into the subvolume across its boundary?

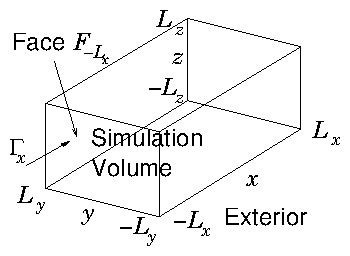
Figure 11.3: Simulating over a volume that is embedded in a wider external region, we need to be able to decide how to inject particles from the exterior into the simulation volume so as to represent statistically the exterior distribution.

Suppose the volume is a cuboid shown in Fig. 11.3. It has 6 faces, each of which is normal to one of the coordinate axes, and located at ±L_x, ±L_y or ±L_z. We'll consider the face perpendicular to x which is at −L_x, so that positive velocity v_x corresponds to moving into the simulation sub-volume. We calculate the rate at which particles are crossing the face into the subvolume. If the distribution function is f(v,x), then the flux density in the +v_x direction is

Γ_x(x) =

⌠
⌡

∞

v_x=0

v_x f(v,x) dv_x dv_ydv_z

(11.13)

and the number entering across the face per unit time (the flux) is

F_{−L_x} =

⌠
⌡

L_y

−L_y

⌠
⌡

L_y

−L_y

Γ_x(−L_x,y,z) dy dz.

(11.14)

Assume that the outer region is steady, independent of time. We proceed by evaluating the six fluxes F_j, using the above expressions and their equivalents for the six different faces. At each time step of the simulation, we decide how many particles to inject into the subvolume from each face. The average number of particles to inject in a timestep ∆t at face j is equal to F_j∆t. If this number is large,⁷⁴ then it may be appropriate to inject just that number (although dealing with the non-integer fractional part of the number needs consideration). But if it is of order unity or even smaller, then that does not correctly represent the statistics. In that case we need to decide statistically at each step how many particles are injected: 0,1,2 ...

It is a standard result of probability theory ⁷⁵ that if events (in this case injections) take place randomly and uncorrelated with each other at a fixed average rate r (per sample, in this case per time-step) then the number n that happens in any particular sample is an integer random variable with "Poisson distribution": a discrete probability distribution

p_n = exp(−r)rⁿ/n! .

(11.15)

The parameter giving the rate, r, is a real number, but the number for each sample, n, is an integer. One can rapidly verify that, since

∞
∑
n=0

rⁿ/n!=exp(r)

, the probabilities are properly normalized:

∑
n

p_n=1

. The mean rate is

∑
n

np_n=r

(as advertized). The variance, it turns out, is also r. So the standard deviation is √r. The value p_n gives us precisely the probability that n particles will need to be injected when the flux is r=F_j. So the first step in deciding injections is to select randomly a number to be injected, from the Poisson distribution eq. (11.15). There are various ways to do this (including library routines). The root-finding approach is easily applied, because the cumulative probability function P_u(u) can be considered to consist of steps of height p_n at the integers n (and constant in between).

Next we need to decide where on the surface each injection is going to take place. If the flux density is uniform, then we just pick randomly a position corresponding to −L_y ≤ y ≤ L_y and −L_z ≤ z ≤ L_z. Non-uniform flux density, however, introduces another distribution function inversion headache. It's more work, but straightforward.

Finally we need to select the actual velocity of the particle. Very importantly, the probability distribution of this selection is not just the velocity distribution function, or the velocity distribution function restricted to positive v_x. No, it it the flux distribution v_xf(v,x) weighted by the normal velocity v_x (for an x-surface) if positive (otherwise zero). If the distribution is separable, f(v)=f_x(v_x)f_y(v_y)f_z(v_z), as it is if it is Maxwellian, then the tangential velocities v_y, v_z, can be treated separately: select two different velocities from the respective distributions. And select v_x (positive) from a probability distribution proportional to v_xf_x(v_x).

If f is not separable, then a more elaborate random selection is required. Suppose we have the cumulative probability distribution of velocities P(v_x,v_y,v_z) for all interesting values of velocity. Notice that if v_xmax, v_ymax, v_zmax denote the largest relevant values of v_x, v_y and v_z, beyond which f=0, then P(v_x,v_ymax,v_zmax) is a function of just one variable v_x, and is the cumulative probability distribution integrated over the entire relevant range of the other velocity components. That is, it is the one-dimensional cumulative probability distribution of v_x. We can convert it into a one-dimensional flux cumulative probability by performing the following integral (numerically, discretely).

F(v_x)

⌠
⌡

v_x

0

v_x′

∂

∂ v_x′

P(v_x′,v_ymax,v_zmax) dv_x′

(11.16)

v_x P(v_x,v_ymax,v_zmax)−

⌠
⌡

v_x

0

P(v_x′,v_ymax,v_zmax) dv_x′.

Afterwards, we can normalize F(v_x) by dividing by F(v_xmax), ariving at the cumulative flux weighted probability for v_x.

We then proceed as follows.

1.	Choose a random v_x from its cumulative flux-weighted probability F(v_x).
2.	Choose a random v_y from its cumulative probability for the already chosen v_x, namely P(v_x,v_y,v_zmax) regarded as a function only of v_y.
3.	Choose a random v_z from its cumulative probability for the already chosen v_x and v_y, namely P(v_x,v_y,v_z) regarded as a function only of v_z.

Naturally for other faces, y and z one has to start with the corresponding velocity component and cycle round the indices. For steady external conditions all the cumulative velocity probabilities need to be calculated only once, and then stored for subsequent time steps.

Discrete particle representation An alternative to this continuum approach is to suppose that the external distribution function is represented by a perhaps large number, N, (maybe millions) of representative "particles" distributed in accordance with the external velocity distribution function. Particle k has velocity v_k and the density of particles in phase space is proportional to the distribution function, that is to the probability distribution. Then if we wished to select randomly a velocity from the particle distribution we simply arrange the particles in order and pick one of them at random. However, when we want the particles to be flux-weighted, in normal direction

say, we must select them with probability proportional to

v_n=

(when positive, and zero when negative). Therefore, for this normal direction we must consider each particle to have appropriate weight. We associate each particle with a real⁷⁶ index r so that when r_k ≤ r < r_k+1 the particle k is indicated. The interval length allocated to particle k is chosen proportional to its weight, so that

r_k+1−r_k ∝

.v_k

. Then the selection consists of a random number draw x, multiplied by the total real index range and indexed to the particle and hence to its velocity: x(r_N+1−r₁)+r₁ = r → k → v_k. The discreteness of the particle distribution will generally not be an important limitation for a process that already relies on random particle representation. The position of injection will anyway be selected differently even if a representative particle velocity is selected more than once.

Worked example: High Dimensionality Integration

Monte Carlo techniques are commonly used for high-dimensional problems; integration is perhaps the simplest example. The reasoning is approximately this. When there are d dimensions, the total number of points in a grid whose size is M in each coordinate-direction is N=M^d. The fractional uncertainty in estimating a one-dimensional integral of a function with only isolated discontinuities, based upon evaluating it at M grid points, may be estimated as ∝ 1/M. If this estimate still applies to multiple dimension integration (and this is the dubious part), then the fractional uncertainty is ∝ ¹/_M=N^−1/d. By comparison, the uncertainty in a Monte-Carlo estimate of the integral based on N evaluations is ∝ N^−1/2. When d is larger than 2, the Monte Carlo square-root convergence scaling is better than the grid estimate. And if d is very large, Monte Carlo is much better. Is this argument correct? Test it by obtaining the volume of a four-dimensional hypersphere by numerical integration, comparing a grid technique with Monte Carlo.

A four-dimensional sphere of radius 1 consists of all those points for which r²=x₁²+x₂²+x₃²+x₄² ≤ 1. Its volume is known analytically; it is π²/2. Let us evaluate the volume numerically by examing the unit hypercube 0 ≤ x_i ≤ 1, i=1,...,4. It is 1/2⁴=1/16th of the hypercube −1 ≤ x_i ≤ 1, inside of which the hypersphere fits; so the volume of of the hypersphere that lies within the 0 ≤ x_i ≤ 1 unit hypercube is 1/16th of its total volume; it is π²/32. We calculate this volume numerically by discrete integration as follows.

A deterministic (non-random) integration of the volume consists of constructing an equally spaced lattice of points at the center of cells that fill the unit cube. If there are M points per edge, then the lattice positions in the dimension i (i=1,...,4) of the cell-centers are x_{i,k_i}=(k_i−0.5)/M, where k_i=1,...,M is the (dimension-i) position index. We integrate the volume of the sphere by collecting values from every lattice point throughout the unit hypercube. A value is unity if the point lies within the hypersphere r² ≤ 1; otherwise it is zero. We sum all values (zero or one) from every lattice point and obtain an integer equal to the number of lattice points S inside the hypersphere. The total number of lattice points is equal to M⁴. That sum corresponds to the total volume of the hypercube, which is 1. Therefore the discrete estimate of the volume of 1/16th of the hypersphere is S/M⁴. We can compare this numerical integration with the analytic value and express the fractional error as the numerical value divided by the analytic value, minus one:

Fractional Error =

⎢
⎢

S/M⁴

π²/32

−1

⎢
⎢

Monte Carlo integration works essentially exactly the same except that the points we choose are not a regular lattice, but rather they are random. Each one is found by taking four new uniform-variate values (between 0 and 1) for the four coordinate values x_i. The point contributes unity if it has r² ≤ 1 and zero otherwise. We obtain a different count S_r. We'll choose to use a total number N of random point positions exactly equal to the number of lattice points N=M⁴, although we could have made N any integer we like. The Monte Carlo integration estimate of the volume is S_r/N.

I wrote a computer code to carry out these simple procedures, and compare the fractional errors for values of M ranging from 1 to 100. The results are shown in Fig. 11.4.

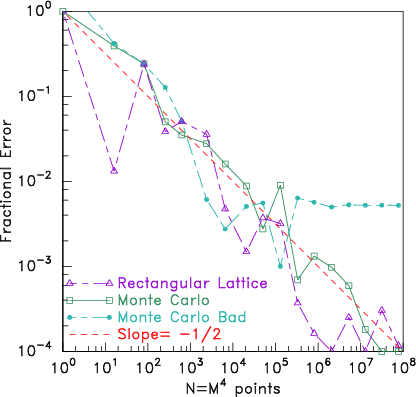
Figure 11.4: Comparing error in the volume of a hypersphere found numerically using lattice and Monte Carlo integration. It turns out that Monte Carlo integration actually does not converge significantly faster than lattice integration, contrary to common wisdom. They both converge approximately like 1/√N (logarithmic slope =−¹/₂). What's more, if one uses a "bad" random number generator (the Monte Carlo Bad line) it is possible the random integration will cease converging at some number, because it gives only a finite-length of independent random numbers, which in this case is exhausted at roughly a million.

Four dimensional lattice integration does as well as Monte Carlo for this sphere. Lattice integration is not as bad as the dubious assumption of fractional uncertainty ¹/_M=N^−1/d suggests; it is more like N^−2/d for d > 1. Only at higher dimensionality than d=4 do tests show the advantages of Monte Carlo integration beginning to be significant. As a bonus, this integration experiment detects poor random number generators.⁷⁷

Exercise 11. Monte Carlo Techniques

1. A random variable is required, distributed on the interval 0 ≤ x ≤ ∞ with probability distribution p(x)=kexp(−kx), with k a constant. A library routine is available that returns a uniform random variate y (i.e. with uniform probability 0 ≤ y ≤ 1). Give formulas and an algorithm to obtain the required randomly distributed x value from the returned y value.

2. Particles that have a Maxwellian distribution

f(v) = n

⎛
⎝

2πk T

⎞
⎠

3/2

exp

⎛
⎝

−

mv²

2kT

⎞
⎠

(11.17)

cross a boundary into a simulation region.

(a) Find the cumulative probability distribution P(v_n) that ought to be used to determine the velocity v_n normal to the boundary, of the injected particles.

(b) What is the total rate of injection per unit area that should be used?

(c) If the timestep duration is ∆t, and the total rate of crossing a face is r such that r∆t = 1, what probability distribution should be used to determine statistically the actual integer number of particles injected at each step?

(d) What should be the probability of 0, 1, or 2 injections?

3. Write a code to perform a Monto Carlo integration of the area under the curve y=(1−x²)^0.3 for the interval −1 ≤ x ≤ 1. Experiment with different total numbers of sample points, and determine the area accurate to 0.2%, and approximately how many sample points are needed for that accuracy.