Chapter 7
Radiation from Charged Particle Interaction with Matter
7.1 Bremsstrahlung
When charged particles collide, they accelerate in each other's
electric field. As a result, they radiate electromagnetic waves. This
type of radiation occurs when a fast electron slows down by
collisions, and so it has acquired the German name Bremsstrahlung
("braking radiation").
7.1.1 Radiation in Collisions, Non-relativistic.
We have analysed collisions of charged particles in some detail in
previous chapters, ignoring the possibility of radiation.
The orbit of the projectile is, classically, a hyperbola. However,
as an approximation, albeit one that will break down if the impact
parameter, b, is small enough, we can ignore the curvature of the
orbit and take the collision to occur with the projectile travelling
along a straight line. This "straight-line-collision" approach we
adopted previously as an approximation for calculating the energy
transfer to a simple harmonic oscillator in a collision. Our present
approach follows a parallel argument.
As it passes the target, the projectile experiences the field of the target,
which accelerates it. When the projectile is far away from the target,
either before or after the collision, the acceleration becomes
negligible. Therefore, the projectile has experienced an "impulse", a
brief period of acceleration. We can estimate the duration of that
impulse as being the time it takes the projectile to travel a distance
of approximately b, namely τ = b/v0, where v0 is the incoming
projectile velocity. On average the impulse is perpendicular to the
projectile velocity.
The total energy radiated in this impulse is given by our previous
formula (4.80)
for the instantaneous radiated power by an accelerated charge,
integrated over the duration of the impulse, τ. Taking the
characteristic value of the acceleration as given by the electric
field force at the closest approach,
|
|
⋅
v
|
= E/ m1 = |
q1 q2
4πϵ0 b2 m1
|
, |
| (7.2) |
we derive an estimate of the radiated energy
|
W ≈ P′τ ≈ |
q14 q22
(4πϵ0)3
|
|
2
3c3
|
|
1
m12 b4
|
|
b
v0
|
= |
q14 q22
(4πϵ0)3
|
|
2
3c3
|
|
1
m12 v0
|
|
1
b3
|
|
| (7.3) |
This is the energy radiated in a single collision with impact
parameter b. To obtain the energy radiated per unit length we
multiply by the density of targets and integrate over impact
parameters to obtain
|
|
dW
dl
|
= n2 | ⌠
⌡
|
|
q14 q22
(4πϵ0)3
|
|
2
3c3
|
|
1
m12 v0
|
|
1
b3
|
2πb db = n2 |
q14 q22
(4πϵ0)3
|
|
4π
3c3
|
|
1
m12 v0
|
| ⎡
⎣
|
1
b
| ⎤
⎦
|
bmax
bmin
|
. |
| (7.4) |
Notice that in this case, there is no need to invoke an upper limit to
the integration, bmax. We can perfectly well let bmax tend
to infinity without any divergence of the integral. The same is not
true of the lower limit. We will either have to invoke the limit on
the classical impact parameter, b90, where our straight-line
approximation breaks down, or, more likely the usual quantum limit
where the wave nature of the projectile becomes important, at
With this quantum cut-off for bmin and infinity for bmax,
the energy radiated becomes
|
|
dW
dl
|
= n2 |
q14 q22
(4πϵ0)3
|
|
4π
3c3
|
|
1
m1 ħ
|
. |
| (7.6) |
7.1.2 Bremsstrahlung from light or heavy particles
So far we have treated the collision maintaining generality in the
projectile and targets but have considered the radiation only from the
projectile. Now we need to discuss what types of
collisions give rise to significant bremsstrahlung. Equation (7.6)
helps this discussion.
First we see that the projectile velocity does not enter into the
formula. The projectile mass, however, is a very important
effect. Light projectiles like electrons or positrons are far more
efficient radiaters (by the inverse mass ratio) than protons or heavy
nuclei, because their acceleration is so much greater.
That said, however, we realize that if a heavy projectile is colliding
with a free electron target, then the electron target will experience an
acceleration and give rise to radiation. This radiation from the
target-particle acceleration is given by the same expression as
before except with the charge and mass of the particles exchanged:
|
|
dW
dl
|
= n2 |
q24 q12
(4πϵ0)3
|
|
4π
3c3
|
|
1
m2 ħ
|
. |
| (7.7) |
Second, concerning targets, there are two effects that tend to cause
the nuclei to dominate as targets in producing bremsstrahlung. The
first effect is plain in eq (7.6). It is that the radiation is
proportional to q22 ∝ Z2, which for heavy atoms is a factor
Z larger than the increase in the radiation caused by there being
Z electrons per atom. The second effect that causes
electron-electron collisions to be inefficient in producing
bremsstrahlung is that the radiated electric fields caused by
accelerations of the projectile electron and the target electron
cancel each other.
Figure 7.1:
Electron-electron bremsstrahlung
radiation wavefronts are out of phase and interfere destructively when
the collision is close compared with the wavelength.
|
k = |
ω
c
|
≈ |
1
cτ
|
≈ |
v0
c b
|
. |
| (7.8) |
Therefore kb ≈ v0/c, in other words, the contributions from
the projectile and target will cancel because kb << 1 if the
incoming velocity is substantially less than the speed of
light. Electron-electron bremsstrahlung is important only for
relativistic electrons. Notice, though, that electron-positron
bremsstrahlung does not produce this field cancellation, so it
can be significant even in the non-relativistic case.
For the predominant case of electron-nucleus bremsstrahlung we can
write eq (7.6) using the definitions of the
fine structure constant α = e2/4πϵ0 ħ c and the
classical electron radius re = e2/4πϵ0 mec2
as
|
|
dW
dl
|
= n2 Z2 me c2 α |
4π
3
|
re2 . |
| (7.9) |
7.1.3 Comparison of Bremsstrahlung and Collisional Energy Loss
The question now arises of the relative importance of bremsstrahlung
in calculating the energy loss of an energetic particle in
matter. This is determined by the ratio of the radiated energy per
unit length, eq(7.6), to the collisional energy loss,
eq(6.45). For non-relativistic bremstrahlung from collisions
with nuclei, so that n2 = na, this ratio is
|
| ⎢
⎢
|
dW
dK
| ⎢
⎢
|
= Z12 Za α |
me v02
m1 c2
|
|
1
3lnΛ
|
, |
| (7.10) |
using the definition of the fine structure constant, α, and
denoting the atomic number of the nuclei as Za.
We see immediately, that bremsstrahlung in non-relativistic collisions
is never an important contributor to the total energy loss,
because even for electron collisions with the heaviest elements,
Z2α ∼ 92/137 ≈ 0.67 and dW/dK is much smaller than
one because of the factors v02/c2 and 1/3lnΛ.
If the projectile is a heavy particle, then the radiation from nuclear
collisions is totally negligible, because of the mass ratio. One might
be concerned then about radiation arising from the acceleration of the
atomic electrons by the passing heavy particle. However, this can
never exceed the energy transferred to the electrons in the collision,
since the acceleration transfers the collisional energy as well as
giving rise to radiation. Formally taking the ratio of
eq(7.7) to the collisional loss we get the same
expression as eq(7.10) except with m1 replaced by the
electron mass, thus confirming that bremsstrahlung is negligible in
non-relativistic energy loss of heavy particles as well as electrons.
We shall see, nevertheless, that electron-nucleus bremsstrahlung can
become important for relativistic electrons.
7.1.4 Spectral Distribution
We may want to calculate the spectrum of the electromagnetic
radiation. It arises as a result of the impulse shape. For a single
collision, the radiation's frequency spectrum will reflect the
frequency spectrum of the impulse. An infinitely sharp impulse has a
uniform frequency spectrum out to infinite frequency. This
accelerating impulse has a duration τ ≈ 2b/v0, and consequently has
an approximately uniform spectrum only out to a cyclic frequency
ν ≈ 1/2τ. (The FWHM of Fourier transform of a square
pulse τ is ∆ν ≈ 1/τ.)
Return therefore to the expression (7.3) for the
radiated energy in a single collision with impact parameter b.
This energy is spread over a total spectral width of approximately
1/2τ so the energy spectral power density is
|
|
dW
dν
|
≈ W2τ = |
q14 q22
(4πϵ0)3
|
|
8
3c3
|
|
1
m12 v02 b2
|
. |
| (7.11) |
This is the energy spectrum radiated in a single collision of
specified impact parameter. If we want to obtain the energy radiated
per unit length, then as usual, we need to multiply by the target
density and integrate 2πb db over all impact
parameters, which gives a logarithmic dependence:
|
|
d2W
dldν
|
= n2 |
q14 q22
(4πϵ0)3
|
|
16π
3c3
|
|
1
m12 v02
|
ln | ⎢
⎢
|
bmax
bmin
| ⎢
⎢
|
. |
| (7.12) |
The bmin will arise because of the wave nature of the
projectile, provided that the corresponding bmin = ħ/ m1 v0
is greater than b90. For any fixed value of the photon frequency,
ν, the maximum impact parameter at which this formula is
appropriate is that parameter for which τ = b/v0 ≈ 1/2ν,
since, as we have already discussed, for larger values of b the
power spectrum falls off rapidly by virtue of the Fourier spectrum of
the time variation of the electric field. Thus
|
Λ = |
bmax
bmin
|
≈ |
m1 v0 v0
ħ2ν
|
= |
πm1 v02
ħω
|
, |
|
Actually, since some energy and momentum is carried away by the photon
radiated, the speed is not simply v0 both before and after the
collision. We could recognize that fact by substituting the average
value of the velocity [1/2]{v0 + √[2(K −ħω)/m1]} instead of v0 in this logarithmic argument,
where K is the initial kinetic energy. If we replace π with 2
in the logarithmic argument and also multiply the main coefficient by
2 (arbitrarily: the above was only an estimate), we obtain:
|
|
d2W
dldν
|
= n2 |
q14 q22
(4πϵ0)3
|
|
32π
3c3
|
|
1
m12 v02
|
ln | ⎢
⎢
⎢
|
ħω
| ⎢
⎢
⎢
|
. |
| (7.13) |
This expression is precisely what is obtained by a non-relativistic
quantum mechanical calculation based on the Born approximation, first
performed by Bethe and Heitler, 1934.
7.1.5 Bremsstrahlung from Relativistic Electrons
It is not straightforward to obtain estimates for bremsstrahlung from
relativistic electrons. A key reason is that since the photon energy
emitted extends from zero up to the electron's incident energy, we
have to deal with photons having energies comparable to the electron
rest mass or more, and hence carrying away momentum that is critical
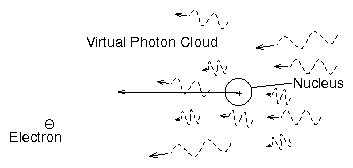
in the scattering process. One way to think about this process is to
regard bremsstrahlung as the scattering of "Virtual Photons"
associated with the field of the nucleus.
This approach, also known as the Weizsäcker-Williams method, after
its earliest proponents, considers bremsstrahlung in the frame of
reference in which the electron is stationary, and the ion moves past
the electron. The electron feels a time-varying electric field
of the ion, whose spectrum we have already discussed in the context of
collisional energy transfer and the oscillator strength. This
time-varying field (at least for velocities near the speed of light)
can be approximated as a spectrum of plane waves. These are the
virtual quanta.
Figure 7.2:
In the rest frame of the electron,
the electric field of the nucleus is regarded as a "cloud" of
virtual photons with a spectrum of energies, which scatter from the electron.
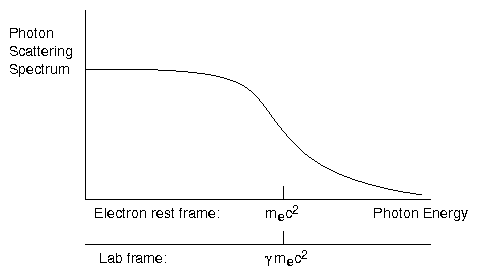
Figure 7.3:
Photon scattering spectrum in the
lab frame can be thought of approximately as a spectum flat to
m
ec
2 in the electron rest frame, Doppler upshifted to γm
ec
2 in the lab frame.
|
|
d2W
dld(ħω)
|
≈ n2 |
q14 q22
(4πϵ0)3
|
|
16
3c3ħ
|
|
1
m12 v02
|
ln | ⎢
⎢
|
2γγ′mec2
ħω
| ⎢
⎢
|
= n2 Z14 Z22 αre2 | ⎛
⎝
|
me
m1
| ⎞
⎠
|
|
16
3
|
| ⎛
⎝
|
mec2
m1v02
| ⎞
⎠
|
lnΛ , |
| (7.14) |
where γ′ = γ− ħω/mec2 is the
relativistic gamma factor of the electron after the photon has been
emitted, and v0 ≈ c, since this is a relativistic collision.
It is possible to write a universal expression for the photon energy
spectrum per unit length, applicable for all energies. The
quantum-mechanical Born-approximation calculations for electron
projectiles yields this expression in the form [Heitler p 250]
|
|
d2W
dld(ħω)
|
= n2 Z22 αre2 |
γ
γ−1
|
B , |
| (7.15) |
where B is a dimensionless function of the ratio ħω/mec2(γ−1), that replaces the factor (16/3)lnΛ.
It is dependent on collision energy (i.e. (γ−1)mec2) and
photon energy, but weakly so.
It has a value of order 15 over most of the photon
spectrum. One can readily verify that this expression has the correct
scaling with velocity at both low and high electron energy.
The magnitude of the cross-section is given by the term
|
αre2 = 0.580×10−31 m−2 = 0.580 millibarn . |
| (7.16) |
(A barn is 10−28 m−2).
7.1.6 Screening and Total radiative loss
We need to account for the screening of the nuclear potential by
surrounding electrons of the atom when the collisions are distant.
The "Thomas-Fermi" potential is an approximation to the screened
nuclear potential that can be approximated as
|
ϕ = |
Ze
4πϵ0 r
|
exp(−r/a) , |
| (7.17) |
with the characteristic length a ≈ 1.4 a0 Z−1/3. This form
of screening is identical to what applies to Coulomb collisional
energy loss etc.
It is most important at low photon energy (relative to the incident
energy) because the distant collisions are most effective there. It
reduces the cross-section (or power radiated) because it essentially
lowers the maximum effective impact parameter to ∼ a.
Estimates of the screening effect can be obtained by putting bmax
equal to a instead of v0/ω, resulting in a logarithmic
factor that for non-relativistic collisions is
|
Λ = |
bmax
bmin
|
≈ |
m1 v0 a
ħ
|
= |
m1 v0 1.4 a0 Z−1/3
ħ
|
= | ⎛
⎝
|
1.4 β
αZ1/3
|
|
m1
me
| ⎞
⎠
|
, |
| (7.18) |
where the final form follows from
Actually screening effects are most important not for non-relativistic
collisions but for relativistic collisions. For relativistic
collisions, we replace the characterisic maximum impact parameter
2γγ′c/ω with a if a is smaller, so that
screening is important. It will be if
|
| ⎛
⎝
|
ω
2γ2 c
| ⎞
⎠
|
| ⎛
⎝
|
1.4 a0
Z1/3
| ⎞
⎠
|
< 1 |
| (7.20) |
This inequality will apply over the entire frequency range up to the
maximum possible photon energy ħω = γm1c2 if the
incident energy satisfies:
|
|
m1 c2
2 γc ħ
|
|
1.4 a0
Z1/3
|
= |
0.7
αγZ1/3
|
|
m1
me
|
< 1 , |
| (7.21) |
using eq (7.19) again. This criterion is γ > 196 /Z1/3
for electron projectiles. When it is satisfied,
the collisions are said to be in the range of "complete screening",
and the logarithmic factor becomes lnΛ ≈ ln(233/Z1/3). [Jackson p722, although our calculation would make
it ln(192/Z1/3)].
For non-relativistic electrons, the radiative energy loss is always
negligible compared with the collisional loss. This is not the case
for strongly relativistic electrons because the total bremsstrahlung
power loss, for the roughly constant spectral power, is proportional
to the total width of the spectrum, i.e. to the collision energy.
Taking the completely screened cross-section case, in which the
logarithmic term and γ/(γ−1) are approximately constant,
the total spectrally integrated energy loss rate is given by
|
|
dW
dl
|
= | ⌠
⌡
|
|
d2W
dld(ħω)
|
d(ħω) = n2 Z22 αre2 | ⎛
⎝
|
16
3
| ⎞
⎠
|
ln | ⎢
⎢
|
233
Z1/3
| ⎢
⎢
|
γmec2 |
| (7.22) |
So writing K=γmec2 for the total electron energy, we get a
slowing down equation
|
− |
dK
dl
|
= K n2 Z22 αre2 | ⎛
⎝
|
16
3
| ⎞
⎠
|
ln | ⎢
⎢
|
233
Z1/3
| ⎢
⎢
|
|
| (7.23) |
If we compare this to the slowing down rate due to collisional effects
(excluding bremsstrahlung) we find that these rates, whose dependence
on the nuclear charge, Z are different, are equal when γ ≈ 200 for air and γ ≈ 20 for lead.
When bremsstrahlung loss predominates over collisional loss, the
energy is sufficient for the screening to be complete. Then the
slowing down rate is constant. That is, the energy loss equation
reduces approximately to
with exponentially decaying solutions K ∝ exp(−l/λ)
having characteristic length:
|
λ = | ⎡
⎣
|
n2 Z22 αre2 | ⎛
⎝
|
16
3
| ⎞
⎠
|
ln | ⎢
⎢
|
233
Z1/3
| ⎢
⎢
| ⎤
⎦
|
−1
|
|
| (7.25) |
The expressions most quoted are slightly different [Heitler, and
subsequently Evans] replacing as follows in the completely screened
limit:
|
| ⎛
⎝
|
16
3
| ⎞
⎠
|
ln | ⎢
⎢
|
233
Z1/3
| ⎢
⎢
|
→ 4 ln | ⎢
⎢
|
183
Z1/3
| ⎢
⎢
|
+ |
2
9
|
= B |
| (7.26) |
although the difference is small, within uncertainties of the whole
approximate approach.
7.1.7 Thick target Bremsstrahlung.
Remarks not typed up.
7.2 Cerenkov Radiation
Maxwell's equations with a dielectric medium:
|
∇ ∧E= |
− ∂B
∂t
|
, ∇ ∧B
= μ0 j + |
1
c2
|
|
∂E
∂t
|
|
| (7.27) |
The current consists of partly the medium polarization
and partly "external" currents, jx, like the particle moving through it.
We combine the polarization current into the [(∂E)/(∂t)] term, using the standard relationship D = ϵ0 E+ P, to get
|
∇ ∧B= μ0jx + μ0 |
∂D
∂t
|
= μ0 jx + |
1
c2
|
|
∂
∂t
|
( ϵE) |
| (7.29) |
where ϵ = dielectric constant = relative permittivity.
Eliminate B:
|
− ∇ ∧( ∇ ∧E) = μ0 |
∂jx
∂t
|
+ |
1
c2
|
|
∂2
∂t2
|
( ϵE) |
| (7.30) |
or
|
− ∇( ∇.E) + ∇2 E− |
1
c2
|
|
∂2
∂t2
|
( ϵE) = μ0 |
∂jx
∂t
|
|
| (7.31) |
This is now a wave-equation but with a source on the right-hand side.
A helpful way to think about Cerenkov radiation is then to regard
the current of the swift particle as coupling to oscillators
consisting of plane waves propagating with wave-vector
k and frequency ω.
Because of the dielectric medium the wave "oscillators"
satisfy k2c2 = ϵω2.
This is the standard result that the refractive index of a transverse wave
in a dielectric is
The wave velocity is [(ω)/k] = c/ϵ1/2,
i.e. the waves travel slower than c. This allows the particle
to couple to the oscillators resonantly. We saw
previously (oscillator strength calculation) that it is
resonance that is required [ |E(ω)|2 is what gives
the energy transfer].
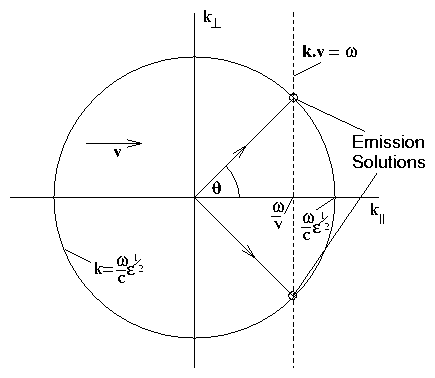
For resonance with a wave ∝ expi (k.x− ωt),
we require a uniformly moving particle (i.e. one without an intrinsic
oscillating frequency) to move such that the phase of the wave is
constant at the particle.
Particle position is r
= vt (+ constant)
so resonance is
|
constant = k . r− ωt = ( k . v− ω) t |
| (7.33) |
i.e. k . v
= ω.
So if we choose a specific frequency ω, we need to satisfy
simultaneously
- k = [(ω)/c] ϵ1/2 (wave dispersion
relation)
- k . v
= ω (resonance with particle)
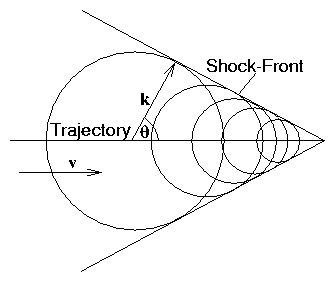
Graphically:
Figure 7.4:
k-coordinates for satisfying
resonance and the dispersion relation
If ϵ is independent of ω, the result is to
form an optical "shock front"
Figure 7.5:
Shock-Front arising from
coherent addition of waves from all along the particle trajectory.
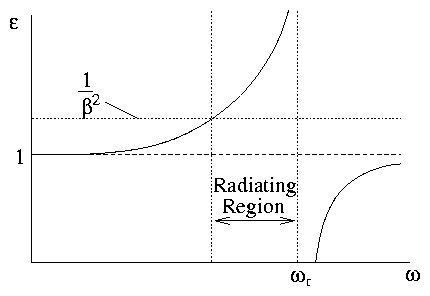
Figure 7.6:
Typical variation of the
relative permittivity of a transparent material.
7.2.1 Coupling Strength
We are interested in transverse waves
| |
|
| | (7.35) |
| |
|
| − k2 E+ |
ω2 ϵ
c2
|
E = μ0 |
∂jx
∂t
|
|
| | (7.36) |
|
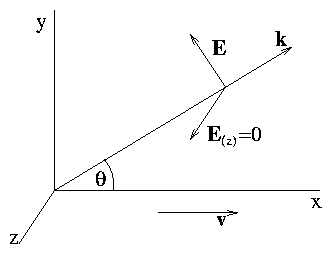
E is perpendicular to k.
If v is in x-direction, then, k = k (cosθ, sinθ)
| |
|
| | (7.37) |
| |
|
| E ( 0, 0, 1 ) are possible polarizations |
| | (7.38) |
|
But coupling to the wave is determined by the vector
[(∂jx)/(∂t)].
Figure 7.7:
Polarization of Cerenkov
emission is purely in the plane of emission. Coupling to
E(z) is
zero.
- It does not couple at all to Ez polarization.
- Coupling to the in-plane polarization,
E
= E(sinθ, cosθ) is proportional to
[(E. j)/Ej] i.e. sinθ
Final point note that driver is [(∂jx)/(∂t)] so that since the spectrum of jx is flat,
because it is a delta function in time, the spectrum of the
drive term is ∝ (i) ω.
All of this can be made rigorous. The result is that the
energy radiated per unit length of path is
|
|
dW
dl
|
= |
q12
4πϵ0
|
|
1
c2
|
| ⌠
⌡
|
ϵ( ω) > [1/(β2)]
|
| ⎛
⎝
|
1 − |
c2
v2ϵ( ω)
| ⎞
⎠
|
ω dω [Frank, Tamm 1937] |
| (7.39) |
and we can identify the terms as
|
1 − |
c2
v2ϵ
|
= 1 − cos2 θ = sin2 θ |
| (7.40) |
i.e. the coupling dependence on radiation angle.
Squared because energy goes like the square of the electric field.
This equation also gives the frequency spectrum of the radiated
power (the integrand) but it is non-zero only for frequencies such
that ϵ > [(c2)/(v2)] or v > phase velocity
[c/(ϵ1/2)].
Energy emitted per unit length is estimated by putting
1 − [(c2)/(v2ϵ)] equal to an average value and so
|
| ⌠
⌡
|
ω2
ω1
|
| ⎛
⎝
|
1 − |
c2
v2ϵ
| ⎞
⎠
|
ω dω ≅ |
1
2
|
[ ω22 − ω21 ] | ⎛
⎜
⎝
|
1 − |
c2
| ⎞
⎟
⎠
|
|
| (7.42) |
where ω2,1 are the upper and lower limits of spectral
region of emission.
| |
|
|
|
q12
4πϵ0
|
|
1
c2
|
|
1
2
|
[ ω22 − ω21 ] | ⎛
⎜
⎝
|
1 − |
c2
| ⎞
⎟
⎠
|
|
| |
| |
|
|
α |
ω2
c
|
|
1
2
|
| ⎡
⎣
|
ħ ω2 − |
ħ ω21
ω2
| ⎤
⎦
|
| ⎛
⎜
⎝
|
1 − |
c2
| ⎞
⎟
⎠
|
|
| |
| |
|
|
α |
ω2
c
|
|
1
2
|
ħω2 | ⎛
⎜
⎝
|
1 − |
c2
| ⎞
⎟
⎠
|
if ω1 << ω2. |
| |
| |
|
| α |
π
λ2
|
ħ ω2 | ⎛
⎜
⎝
|
1 − |
c2
| ⎞
⎟
⎠
|
| ⎛
⎝
|
λ
2π
|
= |
c
ω
| ⎞
⎠
|
|
| | (7.43) |
|
The rough value of this energy per unit length can be estimated
noting that the resonance (where ―ϵ → ∞)
in the optical response of glasses is generally near λ2 = 100 nm ⇒ ħω2 = 12eV, and near
that resonance [(c2)/(v2 ―ϵ)] → 0 so
|
|
dW
dl
|
∼ απ |
1
10−7
|
.12 eV/m = 2.7 ×106 eV/m |
| (7.44) |
This is tiny in comparison with the rate of loss of energy by
other processes.
The number of photons emitted per unit length is even easier
| |
|
|
|
q12
4πϵ0
|
|
1
ħ c2
|
[ ω2 − ω1 ] | ⎡
⎢
⎣
|
1 − |
c2
| ⎤
⎥
⎦
|
|
| | (7.45) |
| |
|
|
α2 π | ⎡
⎣
|
1
λ2
|
− |
1
λ1
| ⎤
⎦
|
| ⎡
⎢
⎣
|
1 − |
c2
| ⎤
⎥
⎦
|
|
| | (7.46) |
| |
|
| α2 π |
1
λ2
|
(for ω2 >> ω1 ). |
| | (7.47) |
|
[And the photon spectral distribution is
|
|
dN
dldω
|
= α |
1
c
|
sin2θ = α |
1
c
|
| ⎡
⎣
|
1 − |
c2
v2ϵ
| ⎤
⎦
|
. ] |
| (7.48) |
Rough estimate of photons (total) / length for λ2 ≅ 100 nm:
Optical range (λ ≅ 400 − 600 nm) contains about
(1/4 − 1/6) = 0.083 times as many
(×sin2θ) so can be as little as [1/25]
of this total ∼ 20 photons/mm.
7.2.2 Energy Spectrum
|
Energy Spectrum proportional to ω | ⎛
⎝
|
1 − |
c2
v2ϵ
| ⎞
⎠
|
|
| (7.50) |
is
- broad and smooth.
- larger at larger ω (smaller λ)
"blue" because
- ω factor
- ϵ increase with ω⇒ 1 −[(c2)/(v2ϵ)] increases
Result: Bluish-White light.
Observed by Marie Curie 1910.
Studied in detail by Cerenkov 1935.
Explained Frank & Tamm 1937 (classical).
Used for detectors starting mid 1940s.