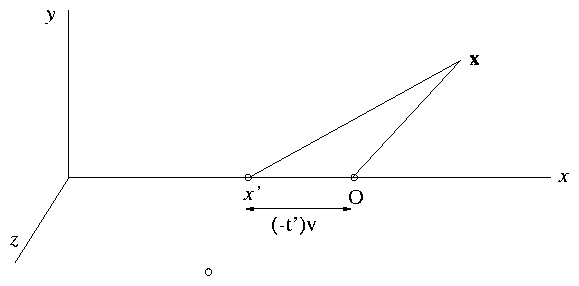Chapter 4
Radiation By Moving Charges
4.1 Potentials and Fields of a moving point charge
The general solution
|
ϕ( x,t ) = |
1
4πϵ0
|
| ⌠
⌡
|
|
[[ ρ]]
| x− x′|
|
d3 x′ |
| (4.1) |
Looks as if it will give the result for a point charge
directly in the same way as the static solution. For a stationary
point charge ρ(x′) = q δ( x′− r), where
r is the charge position, ϕ = [q/(4πϵ0)][1/(|x− r|)].
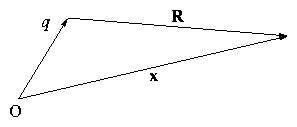
For brevity let's write R ≡ x− r. One might think
for a moving charge ϕ( x,t ) = [q/(4πϵ0)] [[ 1/R ]]
Figure 4.1:
Vector coordinates of charge
and field point.
| |
|
|
|
q
4πϵ0
|
| ⌠
⌡
|
|
δ( x′− r( t′) )
| x− x′|
|
d3x′ , t′ = t − |
| x− x′|
c
|
|
| |
| |
|
|
q
4πϵ0
|
|
1
| x− r( t′) |
|
| ⌠
⌡
|
δ( x′− r( t′) )d3 x′ |
| | (4.2) |
|
where we make use of the fact that the delta function is non-zero only
where its argument is zero, so all the contribution to the integral
comes from the place where
x′ = r(t′), which is where the particle is at retarded
time
i.e.
[This requires self-referential notation which is one reason we
write it [[r]].]
Now we have to do the integral
∫δ( x′− r( t′) )d3x′.
This is not unity because x′ appears inside
r(t′) as well as in x′.
The delta function is defined such that
but now its argument is y = x′− r( t′).
We need to relate d3y to d3x′ for the integral we want.
Consider the gradient of one component:
| |
|
|
∇′( xi′− ri (t′) ) = ∇′[[ x′i −ri ]] |
| |
| |
|
|
[[ ∇′( x′i − ri ) ]] + |
x− x′
c | x− x′|
|
| ⎡
⎣
| ⎡
⎣
|
∂
∂t
|
( x′i − ri ) | ⎤
⎦
| ⎤
⎦
|
|
| |
| |
|
| [[ ∇′xi′]] + |
1
c
|
|
x− x′
| x− x′|
|
| ⎡
⎣
| ⎡
⎣
|
− |
∂ri
∂t
| ⎤
⎦
| ⎤
⎦
|
|
| | (4.5) |
|
[since ri is a function of t but not x′ directly.]
Choose axes such that x′ = ( x1′, x2′,x3′) with component 1 in the R
= x− x′
direction. Then the second term is present only for the x1
component not the other two (because they are ⊥ to x− x′).
Also ( ∇′xi′) = δij.
[i.e. 1 iff i = j].
Thus
| |
|
|
1 + |
1
c
|
| ⎡
⎣
| ⎡
⎣
|
− |
∂r1
∂t
| ⎤
⎦
| ⎤
⎦
|
|
| | (4.6) |
| |
|
| |
|
Consequently
| |
|
|
dy1dy2dy3 = | ⎛
⎝
|
1 − |
1
c
|
| ⎡
⎣
| ⎡
⎣
|
∂r1
∂t
| ⎤
⎦
| ⎤
⎦
| ⎞
⎠
|
dx′1dx′2dx′3 |
| |
| |
|
| ⎡
⎣
| ⎡
⎣
|
1 − |
1
c
|
|
R
R
|
. |
∂r
∂t
| ⎤
⎦
| ⎤
⎦
|
d3x′ |
| | (4.7) |
|
Let's write
|
κ ≡ 1 − |
1
c
|
|
R
R
|
. |
∂r
∂t
|
= 1 − |
1
c
|
|
^
R
|
. v |
| (4.8) |
Then
|
| ⌠
⌡
|
δ( y ) d3 x′ = | ⌠
⌡
|
δ( y ) |
d3y
[[ κ ]]
|
= |
1
[[ κ]]
|
|
| (4.9) |
And finally
|
ϕ( x, t ) = |
q
4πϵ0
|
| ⎡
⎣
| ⎡
⎣
|
1
κR
| ⎤
⎦
| ⎤
⎦
|
|
| (4.10) |
By exactly the same process we can obtain the correct value for
each component of A and in total
|
A( x, t ) = |
μ0 q
4 π
|
| ⎡
⎣
| ⎡
⎣
|
v
κR
| ⎤
⎦
| ⎤
⎦
|
. |
| (4.11) |
( v
= ∂r/∂t ) ,
j
= qvδ.
These expressions are called the "Liénard-Wiechert" potentials
of a moving point charge.
Since the κ correction factor is so important and
the scientific literature is strewn with papers that get it wrong,
let's obtain the result graphically.
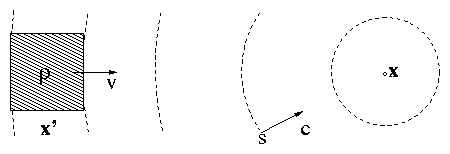
Figure 4.2:
Integral of charge density
over a square-shaped moving charge at
retarded time.
Figure 4.3:
Snapshots as the
integration surface, S, crosses the back and the front of the charge.
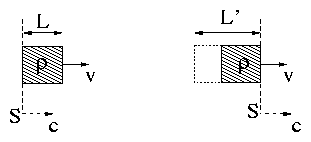
So
|
∆t = |
L
(c − v)
|
and L′ = |
c
c − v
|
L = |
1
|
L |
| (4.13) |
Thus
as before.
Notice that transverse velocity does nothing, and that approximations
implicit in taking S to be planar become exact for a point
charge, with spatial extent → 0.
The quantity κ can also be seen to relate intervals of
time, dt, to the corresponding retarded time intervals,
dt′.
|
t′ = t − |
R′
c
|
or t = t′+ |
R′
c
|
|
| (4.15) |
So
|
|
dt
dt′
|
= 1 + |
1
c
|
|
dR′
dt′
|
. |
| (4.16) |
But
| |
|
|
|
d
dt′
|
| x− r′| = |
d
dt′
|
{ ( x− r′) . ( x− r′)} 1/2 |
| |
| |
|
|
− v. ( x− r′)
R′
|
= − |
v. R′
R′
|
|
| | (4.17) |
|
Hence
|
|
dt
dt′
|
= 1 − |
v. R′
cR′
|
= κ′=[[κ]] |
| (4.18) |
Strictly speaking, it is the value κ′ at retarded time,
when the surface S passes the particle, that is required here if
v is changing.
4.2 Potential of a Point Charge in Uniform Motion
5
Figure 4.4:
Coordinates of a uniformly
moving charge at
r(t)=(vt,0,0).
|
c2 ( −t′)2 = |
c2
v2
|
x′2 = R′2=( x − x′)2 + y2 + z2 . |
| (4.19) |
Gather terms in the x′ form of the equation:
|
x′2 | ⎛
⎝
|
c2
v2
|
− 1 | ⎞
⎠
|
+ 2xx′−( x2 + y2 + z2 ) = 0 . |
| (4.20) |
Solution of quadratic in x′:
|
| ⎛
⎝
|
c2
v2
|
− 1 | ⎞
⎠
|
x′ = − x ± |
⎛
√
|
|
x2 + ( x2 + y2 + z2 ) | ⎛
⎝
|
c2
v2
|
− 1 | ⎞
⎠
|
|
|
| (4.21) |
(where the - sign must be taken).
And so
|
R′ = − |
c
v
|
x′ = |
c
v
|
|
|
x + |
⎛
√
|
|
x2 + ( x2 + y2 + z2 ) | ⎛
⎝
|
c2
v2
|
− 1 | ⎞
⎠
|
|
|
. |
| (4.22) |
We also need the retarded value of κ i.e.
1 − (R′/R′) . (v/c).
and
|
κ′R′ = R′− |
v
c
|
( x − x′) = R′− |
v
c
|
| ⎛
⎝
|
x + |
v
c
|
R′ | ⎞
⎠
|
= | ⎛
⎝
|
1 − |
v2
c2
| ⎞
⎠
|
R′− |
v
c
|
x |
| (4.24) |
Substituting for R′ we get
| |
|
|
|
v
c
|
| ⎧
⎨
⎩
|
x + |
√
|
x2 + ( x2 + y2 + z2 ) ( [(c2)/(v2)] − 1 )
|
− x | ⎫
⎬
⎭
|
|
| |
| |
|
|
|
v
c
|
|
⎛
√
|
|
x2 + ( x2 + y2 + z2 ) | ⎛
⎝
|
c2
v2
|
− 1 | ⎞
⎠
|
|
|
| |
| |
|
| | (4.25) |
|
This is the value at time t=0. At any other time t, the particle
is at the position x=vt instead of at the origin, x=0. Our formula
was developed for the particle at the origin. So to use it we must
move the origin to x=vt, which means we simply have to replace x
in this formula with x − vt. So finally, substituting the general result
for κ′R′ into the Liénard-Wiechert formula we get
|
ϕ( x,t ) = |
q
4πϵ0
|
| ⎡
⎣
| ⎡
⎣
|
1
κR
| ⎤
⎦
| ⎤
⎦
|
= |
q
4 πϵ0
|
|
1
|
|
⎛
√
|
|
|
⎛
√
|
|
| ⎛
⎝
|
x−vt
|
√
|
[
( 1 − v2 /c2 )
]
| ⎞
⎠
|
2
|
+ y2 + z2 |
|
|
|
|
| (4.26) |
See how we have the beginnings of relativity. We get electromagnetic
potential dependence on spatial coordinates that can only be consistent
with the formula in the frame of reference in which the particle is at
rest:
if coordinates transform as
|
x1 = |
x − vt
|
, y1 = y , z1 = z . |
| (4.28) |
This is the (spatial part of the) Lorentz transformation,
incorporating the Fitzgerald contraction in the direction of motion.
Now we also need to recognize there is a vector potential
|
A= |
μ0 q
4π
|
| ⎡
⎣
| ⎡
⎣
|
v
κR
| ⎤
⎦
| ⎤
⎦
|
= |
μ0 q
4π
|
|
v
|
|
⎛
√
|
|
|
⎛
√
|
|
| ⎛
⎝
|
x−vt
|
√
|
[
( 1 − v2 /c2 )
]
| ⎞
⎠
|
2
|
+ y2 + z2 |
|
|
|
|
| (4.29) |
So the electric field has both contributions:
To evaluate these, denote by R1 the quantity
in the denominator of ϕ and A:
|
R1 ≡ |
⎛
√
|
|
| ⎛
⎝
|
x − vt
|
√
|
[ˉ( 1−[(v2)/(c2)])]
| ⎞
⎠
|
2
|
+ y2 + z2 |
|
. |
| (4.31) |
[Note that this is not R′, the retarded radius].
Its derivatives are
|
|
∂R1
∂x
|
= |
x − vt
|
|
1
R1
|
; |
∂R1
∂y
|
= |
y
R1
|
; |
∂R1
∂z
|
= |
z
R1
|
; |
∂R1
∂t
|
= |
− v ( x−vt )
|
. |
| (4.32) |
Consequently
|
∇ |
1
R1
|
= |
−1
R12
|
∇R1 = − |
1
R13
|
| ⎛
⎝
|
x − vt
1 − v2 /c2
|
, y , z | ⎞
⎠
|
|
| (4.33) |
giving
|
−∇ϕ = |
q
4πϵ0
|
|
1
|
|
1
R13
|
| ⎛
⎝
|
x − vt
1 − v2/ c2
|
, y, z | ⎞
⎠
|
|
| (4.34) |
and
|
− |
∂A
∂t
|
= |
q
4πϵ0
|
|
1
|
|
1
R13
|
| ⎛
⎝
|
( − v2 / c2 ) ( x−vt )
( 1 − v2 / c2 )
|
, 0 , 0 | ⎞
⎠
|
|
| (4.35) |
so
|
E= − ∇ϕ− |
⋅
A
|
= |
q
4πϵ0
|
|
1
|
|
1
R13
|
( x−vt , y , z ) . |
| (4.36) |
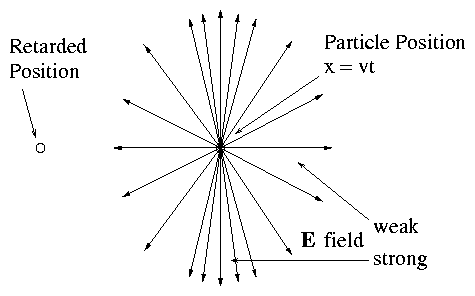
This is a remarkable result. It shows that despite the fact that
contributions to E arise from the retarded position of
the particle, the direction of E is actually radially outward from
the instantaneous (i.e. non retarded) position. The
E field at t=0 is along the radius vector (x,y,z).
Figure 4.5:
Electric field lines of a
charge in uniform motion point outward from the instantaneous (not
retarded) position but the field strength is not symmetric.
|
|
1
|
|
⎛
√
|
|
| ⎛
⎜
⎝
| ⎛
⎜
⎝
|
x−vt
| ⎞
⎟
⎠
|
2
|
+ y2 + z2 | ⎞
⎟
⎠
|
3/2
|
|
|
|
| (4.37) |
which makes it stronger in the perpendicular direction and weaker
in the parallel direction.
The magnetic field may be obtained from B
= ∇∧A by recognizing ∇∧( f v) = − v
∧∇f, if v is constant. Hence, using A
= vϕ/c2,
|
B= − |
v
c2
|
∧∇ϕ = |
v
c2
|
∧ | ⎛
⎝
|
E+ |
∂A
∂t
| ⎞
⎠
|
= |
1
c2
|
v∧E . |
| (4.38) |
[The latter form uses the fact that (A and) [(∂A)/(∂t)] are parallel to v so v∧[(∂A)/(∂t)] = 0].
This expression for the magnetic field
can also be rewritten, by noticing that E is in the direction
of R, R′∧R
=(t−t′) v∧R and t−t′ = R′/c; so v∧E
=(R′c/R′) ∧E.
To summarize:
|
E= |
q
4πϵ0
|
|
x− vt
|
|
⎛
√
|
|
| ⎛
⎜
⎝
| ⎛
⎜
⎝
|
x−vt
| ⎞
⎟
⎠
|
2
|
+ y2 + z2 | ⎞
⎟
⎠
|
3/2
|
|
|
|
| (4.39) |
and
|
B= |
1
c2
|
v∧E= |
1
c R′
|
R′∧E . |
| (4.40) |
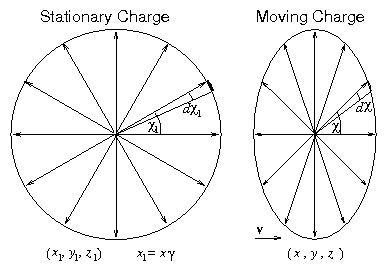
A helpful way to think of the result that the electric field is still
radial but with a non-spherically-symmetric distribution, is to think
about what happens to the field lines when viewed in the lab frame of
reference [components (x,y,z)] compared with a frame of reference in
which the particle is at rest [components (x1,y1,z1)]. It turns
out that the electric field we have calculated is exactly that which
would be obtained by assuming that the spherically symmetric
distribution of field-lines in the rest-frame is simply compressed
together with the rest of space in the x-direction through the
coordinate transform of eq 4.28. This contraction is
illustrated in figure 4.6.
Figure 4.6:
Contraction of space which gives
the electric field-line distribution of a moving charge.
|
tanχ1 = y1/x1 = y/(γx) = (1/γ)tanχ , |
| (4.41) |
where γ = 1/√(1 − v2/c2). Consequently
Now the element of solid angle corresponding to an angle increment
dχ is dΩ = 2πsinχ dχ and
| |
|
|
−d | ⎛
⎜
⎝
|
γ
| ⎞
⎟
⎠
|
= |
γtanχ sec2χ
(γ2+tan2χ)3/2
|
dχ |
| |
| |
|
|
γ
(γ2 cos2χ+sin2χ)3/2
|
sinχ dχ . |
| | (4.43) |
|
So the relationship between corresponding solid-angles is
| |
|
| |
| |
|
|
|
γR3
(γ2 x2 + y2 + z2)3/2
|
dΩ |
| |
| |
|
| | (4.44) |
|
where R=x2+y2+z2.
Therefore if the field-lines are compressed in this purely geometrical
way, the number of field-lines per unit solid angle, which is
proportional to the electric field intensity, in the lab-frame is
equal to the value in the rest-frame times the factor dΩ1/dΩ = γR3/R13. Thus the geometric compression would lead to an
electric field:
This is precisely what we calculated directly from the equations of
the fields. In other words, we can regard the non-symmetric electric
field of eq 4.39 as arising from a compression of space
corresponding to the Lorentz transformation (eq 4.28).
We are not here invoking the Lorentz transformation based on an
understanding of special relativity. In fact the opposite is the
historic situation. Lorentz's transform was part of the prior basis for the
discovery of relativity. See Jackson 1998 pp. 514-518 for
a discussion of electromagnetism as the historic foundation of relativity.
Maxwell's equations are already fully relativistic.
They don't need to be corrected for relativistic effects, the way
Newton's laws require correction for example.
Of course the point is stronger than that: Maxwell's equations
can only be consistent when special relativity applies (i.e.
Lorentz, not Galilean transformations).
We don't have time to cover relativity but we don't have to make a
special point of it since EM equations already are relativisitc.
4.3 Fields of a Generally-Moving Charge
The Lienard Wiechert potentials give the general potential
solution. From them we can obtain the general E and
B fields from a particle moving with arbitrary velocity:
not just uniform v.
Since both potentials and fields depend only on the values
at retarded time, our calculation will be almost the same as for
the uniform motion with the exception that we must use the value of
v at that retarded time and we must account for possible
time-derivatives of v.
Our derivations of ϕ and A go through exactly as before
except that the origin of coordinates is at a point
x′+ v′t′ along the projected path of the
particle if it were to continue past the retarded time with
constant speed v′. [Here we are putting
prime on v to remind that it is the retarded value we
require.]
| |
|
|
|
q
4πϵ0
|
|
1
|
|
√
|
( x−v′t ) + ( y2 + z2 ) ( 1 − [(v′2)/(c2 )] )
|
|
|
| | (4.46) |
| |
|
|
q
4πϵ0 c2
|
|
v′
|
|
√
|
( x−v′t ) +( y2 + z2 ) ( 1 − [(v′2)/(c2 )])
|
|
|
|
| | (4.47) |
|
Now we need to get the fields by differentiation.
We get exactly the same terms as before plus
extra terms arising from the time derivative of v. We could
do this directly by taking into account all the contributions.
Instead, let's do a vector calculation starting with the
Lienard-Wiechert forms:
|
ϕ = |
q
4πϵ0
|
| ⎡
⎣
| ⎡
⎣
|
1
κR
| ⎤
⎦
| ⎤
⎦
|
; A
= |
q
4πϵ0c2
|
| ⎡
⎣
| ⎡
⎣
|
v
κR
| ⎤
⎦
| ⎤
⎦
|
. |
| (4.48) |
|
E= − ∇ϕ− |
∂A
∂t
|
= |
q
4πϵ0
|
| ⎧
⎨
⎩
|
− ∇ | ⎡
⎣
| ⎡
⎣
|
1
κR
| ⎤
⎦
| ⎤
⎦
|
− |
1
c2
|
|
∂
∂t
|
| ⎡
⎣
| ⎡
⎣
|
v
κR
| ⎤
⎦
| ⎤
⎦
| ⎫
⎬
⎭
|
|
| (4.49) |
Again, extreme care must be taken with the differentials. For any
function f(x,t),
| |
|
|
∇f ( x, t − [( |x− x′|)/c] ) |
| |
| |
|
| [[ ∇f ]] − | ⎡
⎣
| ⎡
⎣
|
∂f
∂t
| ⎤
⎦
| ⎤
⎦
|
|
1
c
|
∇[[ | x− x′| ]] |
| | (4.50) |
|
This is not the same situation as we had before. There
we had ∇′ i.e. gradient with respect to retarded
position, x′, keeping x and t fixed. Here we
are talking about gradient w.r.t. x keeping t fixed.
Apply the above equation to the function |x− x′| which is,
strictly speaking, [[ |x− r| ]] or [[ R ]]. We get
|
∇[[ |x− r| ]] = [[ ∇| x− r| ]] − | ⎡
⎣
| ⎡
⎣
|
∂
∂t
|
| x− r| | ⎤
⎦
| ⎤
⎦
|
|
1
c
|
∇[[ |x− r| ]] |
| (4.51) |
i.e.
|
| ⎡
⎣
| ⎡
⎣
| ⎛
⎝
|
1 − |
R′
R′
|
. |
v
c
| ⎞
⎠
| ⎤
⎦
| ⎤
⎦
|
∇[[|x− r|]] = [[ ∇| x− r| ]] |
| (4.52) |
So
|
∇[[ R ]] = | ⎡
⎣
| ⎡
⎣
|
1
κ
|
∇R | ⎤
⎦
| ⎤
⎦
|
= | ⎡
⎣
| ⎡
⎣
|
R
κR
| ⎤
⎦
| ⎤
⎦
|
. |
| (4.53) |
Then returning to the general identity (4.50), substitute for ∇[[R]]
to find:
|
∇[[ f ]] = [[ ∇f ]] − | ⎡
⎣
| ⎡
⎣
|
∂f
∂t
| ⎤
⎦
| ⎤
⎦
|
|
1
c
|
| ⎡
⎣
| ⎡
⎣
|
R
κR
| ⎤
⎦
| ⎤
⎦
|
|
| (4.54) |
or finally
|
∇[[ f ]] = | ⎡
⎣
| ⎡
⎣
|
∇f − |
R
cκR
|
|
∂f
∂t
| ⎤
⎦
| ⎤
⎦
|
. |
| (4.55) |
For the time derivative, we proceed more directly, recognizing that
[(∂f)/(∂t)] means differential of f with respect to its
second argument, but [(∂)/(∂t)][[f]] means
differential with respect to t of a function whose second
(time-like) argument
is t′. Thus
|
|
∂
∂t
|
[[ f ]] = |
∂
∂t
|
f ( x, t′) = |
dt′
dt
|
|
∂
∂t′
|
f( x, t′) = |
1
κ′
|
| ⎡
⎣
| ⎡
⎣
|
∂f
∂t
| ⎤
⎦
| ⎤
⎦
|
|
| (4.56) |
using equation (4.18), dt/dt′=κ′=[[κ]].
Therefore we have generally
|
|
∂
∂t
|
[[ f ]] = | ⎡
⎣
| ⎡
⎣
|
1
κ
|
|
∂f
∂t
| ⎤
⎦
| ⎤
⎦
|
. |
| (4.57) |
Ok, now we have the general derivative tools to evaluate E. It becomes
|
E= |
q
4πϵ0
|
| ⎡
⎣
| ⎡
⎣
|
− ∇ | ⎛
⎝
|
1
κR
| ⎞
⎠
|
+ |
R
cκR
|
|
∂
∂t
|
| ⎛
⎝
|
1
κR
| ⎞
⎠
|
− |
1
c2κ
|
|
∂
∂t
|
| ⎛
⎝
|
v
κR
| ⎞
⎠
| ⎤
⎦
| ⎤
⎦
|
. |
| (4.58) |
With everything inside the retardation operator, it is safe to
proceed with algebra using straightforward derivatives with respect to
the spatial and temporal arguments of the functions, and the fact that
∂R/∂t = −∂r/∂t = −v.
In particular,
| |
|
| | (4.59) |
| |
|
| | (4.60) |
| |
|
|
|
∂R
∂t
|
− |
1
c
|
|
∂R
∂t
|
. v− |
R
c
|
. |
∂v
∂t
|
|
| |
| |
|
| | (4.61) |
|
where dot denotes [(∂)/(∂t)]. The terms in E
are then
| |
|
|
|
1
κ2 R2
|
∇( κR ) = |
1
κ2R2
|
| ⎛
⎝
|
R
R
|
− |
v
c
| ⎞
⎠
|
|
| | (4.62) |
| |
|
|
− |
1
cκ3R3
|
R |
∂
∂t
|
( κR ) = − |
1
cκ3R3
|
R | ⎛
⎝
|
⋅
R
|
+ |
v2
c
|
− |
1
c
|
R. |
⋅
v
| ⎞
⎠
|
|
| | (4.63) |
| |
|
|
1
c2κ3R2
|
| ⎛
⎝
|
⋅
R
|
+ |
v2
c
|
− |
1
c
|
R. |
⋅
v
| ⎞
⎠
|
v− |
1
c2κ2R
|
|
⋅
v
|
|
| | (4.64) |
|
Gathering terms together, denoting ∧R = [(R)/R], and using
· R = −v.R,
we get
|
E= |
q
4πϵ0
|
| ⎡
⎢
⎣
| ⎡
⎢
⎣
|
1
κ3R2
|
| ⎛
⎝
|
^
R
|
− |
v
c
| ⎞
⎠
|
| ⎛
⎝
|
1 − |
v2
c2
| ⎞
⎠
|
− |
1
cκ3R
|
| ⎧
⎨
⎩
|
κ |
c
|
− | ⎛
⎝
|
^
R
|
− |
v
c
| ⎞
⎠
|
| ⎛
⎜
⎝
|
^
R
|
. |
c
| ⎞
⎟
⎠
| ⎫
⎬
⎭
| ⎤
⎥
⎦
| ⎤
⎥
⎦
|
|
| (4.65) |
or alternatively, using vector triple product identities,
|
E= |
q
4πϵ0
|
| ⎡
⎢
⎣
| ⎡
⎢
⎣
|
1
κ3R2
|
| ⎛
⎝
|
^
R
|
− |
v
c
| ⎞
⎠
|
| ⎛
⎝
|
1 − |
v2
c2
| ⎞
⎠
|
+ |
1
cκ3R
|
|
^
R
|
∧ | ⎡
⎢
⎣
| ⎛
⎝
|
^
R
|
− |
v
c
| ⎞
⎠
|
∧ |
c
| ⎤
⎥
⎦
| ⎤
⎥
⎦
| ⎤
⎥
⎦
|
. |
| (4.66) |
The magnetic field is B
= ∇∧A which becomes
| |
|
|
|
q
4πϵ0c2
|
| ⎧
⎨
⎩
|
∇∧ | ⎡
⎣
| ⎡
⎣
|
v
κR
| ⎤
⎦
| ⎤
⎦
| ⎫
⎬
⎭
|
|
| |
| |
|
|
q
4 πϵ0c2
|
| ⎡
⎣
| ⎡
⎣
|
∇∧ | ⎛
⎝
|
v
κR
| ⎞
⎠
|
− |
R
cκR
|
∧ |
∂
∂t
|
| ⎛
⎝
|
v
κR
| ⎞
⎠
| ⎤
⎦
| ⎤
⎦
|
, |
| | (4.67) |
|
by an identity directly analogous to the one we showed for
gradient. Also, using eq 4.62 and noting that terms of
the form v∧v and ∧R∧∧R can be inserted or
removed at will since they are always zero we have
| |
|
|
− v∧∇ | ⎛
⎝
|
1
κR
| ⎞
⎠
|
= |
1
κ2R2
|
v∧ | ⎛
⎝
|
^
R
|
− |
v
c
| ⎞
⎠
|
|
| |
| |
|
| − |
1
κ2R2
|
c |
^
R
|
∧ | ⎛
⎝
|
^
R
|
− |
v
c
| ⎞
⎠
|
= − c |
^
R
|
∧∇ | ⎛
⎝
|
1
κR
| ⎞
⎠
|
. |
| | (4.68) |
|
Hence
|
B= |
q
4πϵ0c2
|
| ⎡
⎣
| ⎡
⎣
|
−c |
^
R
|
∧∇ | ⎛
⎝
|
1
κR
| ⎞
⎠
|
− |
^
R
|
∧ |
1
cκ
|
|
∂
∂t
|
| ⎛
⎝
|
v
κR
| ⎞
⎠
| ⎤
⎦
| ⎤
⎦
|
= |
1
c
|
| ⎡
⎣
| ⎡
⎣
|
^
R
| ⎤
⎦
| ⎤
⎦
|
∧E , |
| (4.69) |
by comparison with our expression (4.58) for E.
Summarizing our results, the fields due to a point charge q moving
with variable velocity v such that the radius vector from the charge
to the field-point is R may be expressed using
κ ≡ 1−∧R.v/c as:
| |
|
|
|
q
4πϵ0
|
| ⎡
⎢
⎣
| ⎡
⎢
⎣
|
1
κ3R2
|
| ⎛
⎝
|
^
R
|
− |
v
c
| ⎞
⎠
|
| ⎛
⎝
|
1 − |
v2
c2
| ⎞
⎠
|
+ |
1
cκ3R
|
|
^
R
|
∧ | ⎡
⎢
⎣
| ⎛
⎝
|
^
R
|
− |
v
c
| ⎞
⎠
|
∧ |
c
| ⎤
⎥
⎦
| ⎤
⎥
⎦
| ⎤
⎥
⎦
|
|
| | (4.70) |
| |
|
| | (4.71) |
|
There are several different forms of these expressions, useful
to illustrate different aspects of the fields of a moving point
charge. See Jackson and Feynman for discussion of some of these.
4.4 Radiation from Moving Charges
4.4.1 Near Field and Radiation Terms
The form for E that we obtained was exhibited in a way that
had 2 separate terms. The first of those terms does not contain
· v while the second is proportional to · v. Therefore
the first term is exactly what would be obtained for uniform motion
· v = 0 (although this is not obvious when comparing with our
earlier formula expressed in coordinates).
Also, everything inside the brackets is dimensionless (∧R, [(v)/c]) except [1/(κ3R2)] and
[1/(cκ3R)][(· v)/c]. These factors decide
the behaviour of their respective terms at large field-point
distances, R. The `static' (constant v) term is
∝ [1/(R2)] but the · v term is
∝ 1/R. Consequently, the Poynting vector
is
|
E∧H = |
1
μ0
|
E∧B= |
1
μ0c
|
E∧ | ⎛
⎝
| ⎡
⎣
| ⎡
⎣
|
^
R
| ⎤
⎦
| ⎤
⎦
|
∧E | ⎞
⎠
|
∝ |
1
R4
|
or |
1
R2
|
|
| (4.72) |
respectively.
If we ask about the total EM power flux across a spherical surface
far from the charge, that value scales like the surface area
4 πR2 tims E∧H. Thus power flux
∝ [1/(R2)] for the constant v term, and ∝ 1
for the · v term.
We see then, that the constant-v term gives rise to vanishingly
small power flux far from the charge but the · v term gives
rise to finite power flux even at infinity. This distinction
requires us to regard these two terms as the
"near field" term:
and "radiation" term:
A charged particle radiates only if
it accelerates.
4.4.2 Radiation into a Specific Solid-angle
Having identified just the 1/R term as the radiation term, we
will drop the other, near field, term from consideration.
Imagine, then, a sphere of radius R surrounding the retarded
position of the particle. The Poynting vector of the radiation
term there is
| |
|
|
E∧ | ⎛
⎝
| ⎡
⎣
| ⎡
⎣
|
^
R
| ⎤
⎦
| ⎤
⎦
|
∧E | ⎞
⎠
|
/ c μ0 = ( E2/cμ0 ) | ⎡
⎣
| ⎡
⎣
|
^
R
| ⎤
⎦
| ⎤
⎦
|
− | ⎛
⎝
|
E. | ⎡
⎣
| ⎡
⎣
|
^
R
| ⎤
⎦
| ⎤
⎦
| ⎞
⎠
|
E/cμ0 |
| |
| |
|
|
1
cμ0
|
E2 | ⎡
⎣
| ⎡
⎣
|
^
R
| ⎤
⎦
| ⎤
⎦
|
= cϵ0 E2 | ⎡
⎣
| ⎡
⎣
|
^
R
| ⎤
⎦
| ⎤
⎦
|
, |
| | (4.75) |
|
where the last two forms recognize that the radiation term has E
perpendicular to [[ ∧R]].
Radiated energy thus crosses the sphere, normal to its surface with a
local intensity (energy/unit area/unit time) E2/cμ0, with
E given by the second term of eq (4.70).
One is very often interested in the power radiated per unit solid angle,
Ωs, subtended by the area at the point of radiation.
By definition of solid angle, a small area of the sphere, A, subtends
a solid angle A/R2. Consequently the power per unit solid angle
is R2E2/cμ0. The extra term R2 cancels the R2
occurring in E2, leaving an expression independent of the
radius, R, of the sphere. By convention we can write the power per
unit solid angle using the notation
|
|
dP
dΩs
|
= |
R2E2
cμ0
|
= |
q2
4πϵ0
|
|
1
4πc
|
| ⎢
⎢
⎢
| ⎡
⎢
⎣
| ⎡
⎢
⎣
|
1
κ3
|
|
^
R
|
∧ | ⎧
⎨
⎩
| ⎛
⎝
|
^
R
|
− |
v
c
| ⎞
⎠
|
∧ |
c
| ⎫
⎬
⎭
| ⎤
⎥
⎦
| ⎤
⎥
⎦
| ⎢
⎢
⎢
|
2
|
|
| (4.76) |
4.4.3 Radiation from Non-relativistic Particles: Dipole Approximation
Considerable algebraic simplifications occur when v/c << 1
and so we can approximate (∧R− v/c) ≅ ∧R, and
κ = 1.
Then
|
|
dP
dΩs
|
= |
q2
4πϵ0
|
|
1
4πc
|
| |
^
R
|
∧ | ⎛
⎜
⎝
|
^
R
|
∧ |
c
| ⎞
⎟
⎠
|
|2 = |
q2
4 πϵ0
|
|
1
4πc
|
| ⎛
⎜
⎝
|
c
| ⎞
⎟
⎠
|
2
|
sin2 α |
| (4.77) |
where α is the angle between ∧R, the direction of the
solid angle (propagation), and · v, the acceleration.
An integration of the total radiated power over the entire sphere
(all solid-angles) can readily be done. Taking the direction of
· v to be the polar direction, the integral is such that
So, noting that
|
| ⌠
⌡
|
sin2α 2πsinα dα = 2 π | ⌠
⌡
|
( 1 − cos2 α) sinα dα = 2 π | ⎡
⎣
|
−cosα+ |
1
3
|
cos3α | ⎤
⎦
|
π
0
|
= |
8π
3
|
, |
| (4.79) |
we get
|
P = | ⌠
⌡
|
|
dP
dΩs
|
dΩs = |
q2
4 πϵ0
|
|
2
3c
|
| ⎛
⎜
⎝
|
c
| ⎞
⎟
⎠
|
2
|
. |
| (4.80) |
This expression for the total radiation from a non-relativistic
accelerated charge is known as Larmor's formula.
The non-relativistic expressions for P and dP/dΩs are
often referred to as the "dipole approximation" because they
are exactly what is obtained for the radiation from a
stationary oscillating dipole electric distribution when the
electric dipole moment p, is such that
Thus this radiation pattern and intensity is what is obtained also
from dipole antennas that are much smaller than the radiation
wavelength.
4.5 Radiation from Relativistic Particles
The general expression for radiation by an accelerated particle,
without invoking approximations requiring v << c, is given by
eq (4.76). However an important distinction must be drawn in
discussions of energy per unit time between expressions based
on time-at-field-point, t, such as eq (4.76), and expressions
referring to time-at-particle, retarded time t′. If we
want to know how much energy a particle is radiating per unit
time-at-particle, which is what we do want if, for example, we
want to calculate how rapidly the particle is losing energy,
or indeed if we want to calculate the total energy radiated per
unit volume by adding up the energy radiated by all the particles
in that volume, then we must multiply expressions for energy
per time-at-field-point by the ratio dt/dt′ = κ.
This conversion lowers the power of κ in the denominator by
one. We shall work henceforth with such expressions of energy per unit
time-at-particle
and will indicate this by a prime on the power: P′.
Even so, we still have a factor κ5 in
the denominator of dP′/dΩs. This factor is the
most important effect. Since κ = 1 − ∧R. v/c =
1 − βcosθ, when we are dealing with particles moving
near the speed of light, κ becomes extremely small when
θ ≅ 0, that is for radiation in the direction along
the particle's velocity. As a result, the radiation is greatly
enhanced in this forward direction, an effect that is sometimes
called the relativistic "headlight" effect.
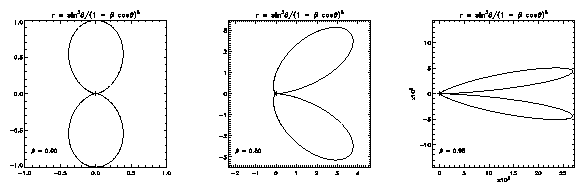
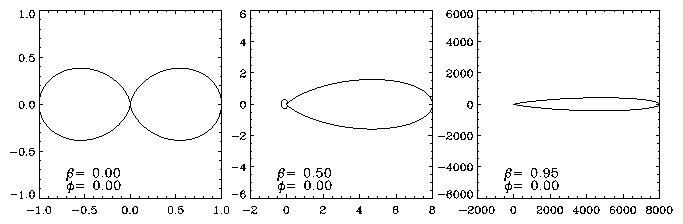
4.5.1 Acceleration Parallel to v
The simplest case algebraically is when v and · v are
parallel. The radiation is then rotationally symmetric about this
direction. The κ factor is then the only difference
from the dipole formula eq (4.77):
|
|
dP′
dΩs
|
= |
q2
4πϵ0
|
|
4πc3
|
|
sin2 θ
( 1 − βcosθ)5
|
. |
| (4.82) |
Figure 4.7:
Polar plots of the radiation
intensity as a function of direction, with acceleration parallel to
v, for different values of β = v/c. Velocity is in the x-direction.
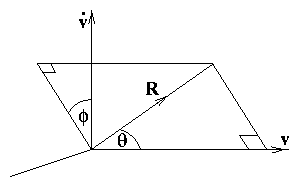
4.5.2 Acceleration Perpendicular to v
Figure 4.8:
Definition of the angles for
radiation when
· v is perpendicular to
v.
|
|
dP′
dΩs
|
= |
q2
4πϵ0
|
|
4πc3
|
|
1
( 1 − βcosθ)3
|
| ⎡
⎣
|
1 − |
sin2θcos2ϕ( 1−β2 )
(1 − βcosθ)2
| ⎤
⎦
|
|
| (4.83) |
where θ is the angle of ∧R with respect to
v and ϕ is the polar angle of ∧R about
v measured with respect to · v as zero.
Figure 4.9:
Polar plots of the radiation
intensity as a function of direction, with acceleration perpendicular
to
v, for the case where
∧R lies in the plane of
v and
· v.
4.5.3 Total Radiated Power
The general expression (4.76) can be integrated over solid angles
by elementary but tedious methods to obtain
| |
|
|
|
q2
4πϵo
|
|
2
3c
|
γ6 | ⎡
⎢
⎣
| ⎛
⎜
⎝
|
c
| ⎞
⎟
⎠
|
2
|
− | ⎛
⎜
⎝
|
c
|
∧ |
v
c
| ⎞
⎟
⎠
|
2
| ⎤
⎥
⎦
|
|
| |
| |
|
|
q2
4πϵ0
|
|
2
3c
|
γ4 | ⎡
⎢
⎣
| ⎛
⎜
⎝
|
c
| ⎞
⎟
⎠
|
2
|
− | ⎛
⎜
⎝
|
c
|
. |
v
c
| ⎞
⎟
⎠
|
2
| ⎤
⎥
⎦
|
, |
| | (4.84) |
|
the first form of which was obtained by Lienard (1898). These
two alternate forms are convenient for
obtaining the power when · v
is parallel to v:
and · v is perpendicular to v:
|
P′ = |
q2
4πϵ0
|
|
2
3c
|
|
c2
|
γ4 . |
| (4.86) |
These expressions give important quantitative information
about the rate of energy loss by a charge undergoing
acceleration.
The first thing we can see is that a charge could never be
accelerated through the velocity c, because γ→∞ at β→ 1 and so infinite amounts of
radiation would be emitted. This remark is quite independent
of Einstein's theory of relativity which shows that the mass
becomes infinite as β→ 1. Thus in 1898
when Lienard obtained his expression he already could have deduced that
a charge could not be accelerated past v = c.
Second, let us compare the rate of radiative energy loss to
the energy gain from an accelerating electrostatic force.
Figure 4.10:
Comparing the radiative energy
loss to the energy gained from force during acceleration due to a
nearby charge.
accounting for the relativistic mass increase. Supposing · v
to be parallel v, the rate of radiative loss is
|
P′ = |
q2
4πϵ0
|
|
2
3c3
|
|
Z2q4
( 4πϵ0 )2
|
|
1
r4
|
|
γ4
m02
|
. |
| (4.88) |
This will equal the rate of gain of energy due to acceleration,
namely
when
|
| ⎛
⎝
|
Zq2
4πϵ0 r
| ⎞
⎠
|
2
|
= Z |
3β( m0c2 )2
2 γ4
|
, |
| (4.89) |
or
|
|
Zq2
4πϵ0 r
|
= | ⎛
⎝
|
3Zβ
γ4
| ⎞
⎠
|
1/2
|
m0c2 . |
| (4.90) |
The left-hand side, here, is the potential energy of the charge and
the right-hand side is a square-root factor times the rest-mass of the
charge (expressed as an energy). For modestly relativistic particles,
when we can take the square-root factor to be of order unity, we
therefore see that radiation would begin to have an important effect
relative to the parallel acceleration only when an electron (for
example) is in a potential well at a depth ∼ m0c2 = 511 keV.
Remembering that the binding energy of a hydrogen atom is only 13.6 eV
this could happen only in the most exotic of situations (e.g. inner
shells of heavy elements). Of course those situations would really
have to be treated by quantum mechanics. Moreover these immensely
strong electric fields ( ∼ 1020 V/m) are never even approached
in present accelerators. So radiation caused by acceleration parallel
to v, such as in a linac, is never a serious consideration.
If v
is perpendicular to · v, however, the lowest order energy gain
by the acceleration is zero. Compared with this the radiation may
well be important. In the atomic force-field
|
P′ = |
q2
4πϵ0
|
|
2
3c3
|
|
Z2q4
( 4πϵ0 )2
|
|
1
r4
|
|
γ2
m02
|
|
| (4.91) |
and the classical kinetic energy in a circular orbit at radius
r is
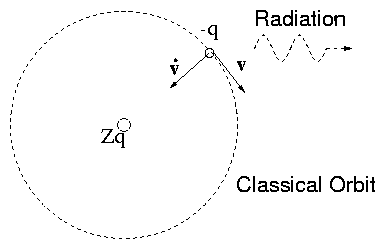
Figure 4.11:
Radiation from a particle
moving in a circular orbit arises from its perpendicular acceleration.
| |
|
|
|
1
2
|
|
Zq2
4πϵ0r
|
| ⎡
⎣
|
q2
4πϵ0
|
|
2c
3
|
| ⎛
⎝
|
Zq2
4πϵ0r
| ⎞
⎠
|
2
|
|
1
r2
|
|
γ2
m02c4
| ⎤
⎦
|
−1
|
|
| |
| |
|
|
( m0c2 )2
2γ2
|
|
3r
2c
|
Z | ⎛
⎝
|
Zq2
4πϵ0r
| ⎞
⎠
|
−2
|
= |
( m0c2 )2
I2
|
Z |
r
c
|
, |
| | (4.93) |
|
where I is the binding energy of the particle in this circular
orbit. For a "classical" hydrogen atom circular orbit,
I = 13.6eV, Z=1, and r = a0 = 5.29 ×10−11 m
(the Bohr radius) we get τ = 1.5 ×10−9s. Thus
the rate of loss of energy by an electron in a "classical"
Bohr orbit is such that the electron would spiral into the
nucleus in a few nanoseconds. This, of course, was one of
the key problems with classical electrodynamics that physics
faced in the early
1900s, which prompted
the eventual discovery of quantum mechanics.
As an immediately practical matter, we can also ask how fast a
particle radiates energy because of being accelerated by a magnetic
field, in the circular orbit of a cyclotron, for example.
In this case, the acceleration is · v = v2/d, where d
is the orbit radius. The power radiated is then, from eq (4.86),
|
P′ = |
q2
4πϵ0
|
|
2
3c
|
|
v4
c2 r2
|
γ4 = |
q2
4πϵ0
|
|
2c
3
|
|
β4 γ4
r2
|
. |
| (4.94) |
For a relativistic particle (β ≅ 1) the power therefore
increases proportional to the fourth power of the energy (γ4),
and the energy loss per orbit for electrons moving with radius of
curvature r can be written numerically
in the form
|
δE / MeV = 8.8 ×10−2 |
( E/GeV )4
( r/meters )
|
. |
| (4.95) |
This amounts to a major limitation for electron storage rings and
accelerators above a few GeV energy. Jackson (p 668) cites
the Cornell electron synchrotron with r = 100 meters having a loss
of 8.8 MeV per turn at 10 GeV. The MIT Bates accelerator storage ring
is designed for up to 1 GeV energy. With a bend radius of 9.1 m the
loss is 9.8 keV per turn which is compensated by an accelerating stage
within the ring.
4.6 Scattering of Electromagnetic Radiation
4.6.1 Thomson Scattering
We have seen that a non-relativistic accelerated charge radiates
according to (eq 4.77),
|
|
dP
dΩs
|
= |
q2
4 πϵ0
|
|
1
4πc
|
| ⎛
⎜
⎝
|
c
| ⎞
⎟
⎠
|
2
|
sin2 α , |
| (4.96) |
where α is the angle between the direction of radiation and
the direction of the acceleration, · v.
If the acceleration arises from an electric field Ei, then
Therefore the power radiated per unit solid angle from a single
electron can be written:
|
|
dP
dΩs
|
= |
e2
4 πϵ0
|
|
1
4πc
|
| ⎛
⎝
|
e
me c
|
Ei | ⎞
⎠
|
2
|
sin2α = | ⎛
⎝
|
e2
4 πϵ0 me c2
| ⎞
⎠
|
2
|
c ϵ0 Ei2 sin2α . |
| (4.98) |
The combination of parameters arising in the last form of this equation,
has the dimensions of length, and is called the classical electron
radius.
A steady electric field will not give rise to radiation that is
particularly interesting, but if the electric field is oscillating, it
will give rise to radiation that is at a corresponding frequency.
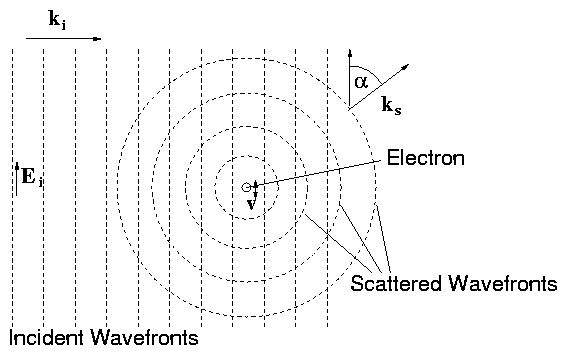
Figure 4.12:
Schematic illustration of the
process of Thomson Scattering.
|
si = |E∧B/μ0| = |
1
cμ0
|
Ei2 = c ϵ0 Ei2 , |
| (4.100) |
and we evaluate it at retarded time t′ (i.e. at the time necessary to
give rise to radiation at the field point at later time t).
Therefore the scattered power per unit solid angle from a single
electron can be written:
The differential (energy) scattering cross-section is the
ratio of dP/dΩs to the incident power density si. One can
rapidly verify that this definition is in accord with the standard
definition of a cross-section: that it should be such that the number
of collisions per unit length is equal to the product of the
cross-section and the density of targets. In this case the
"projectiles" are represented by the incident energy of the wave.
The projectiles can be considered to have a flux density proportional
the wave power flux density, si. An alternative view of this
cross-section is to regard it as the area across which the incident
power flux density would have to flow in order to give rise to the
power scattered.
The
cross-section is
where α is the angle between the scattering direction and the
electric field (i.e. the polarization direction) of the incident wave.
Integrated over all scattering angles this expression yields the total
Thomson scattering cross-section
If the electron is stationary apart from the oscillation that the wave
imparts to it, then the scattered radiation will have exactly the same
frequency (in this classical approximation) as the incident
wave. However if the electron is moving prior to its perturbation by
the incident wave, then there will be a Doppler shift of the scattered
frequency both because the moving electron will experience the
incident wave at a different frequency and because its radiation will
be Doppler shifted at the observer. These two effects give a scattered
frequency ωs that is related to the incident frequency
ωi by
|
ωs = ωi +(ks −ki).v0 = ωi |
|
, |
| (4.104) |
where ki and ks are the wave-vectors of the incident
and scattered waves respectively, whose magnitudes are
ki=ωi/c and ks=ωs/c, and hats indicate unit
vectors. The numerator and denominator of the fractional form for
ωs represent the two Doppler shifts just referred to.
This one-to-one relationship between the scattered frequency and the
component of the electron velocity along the direction ks−ki is extremely helpful in plasma diagnostic
applications. The velocity distribution of the electrons is directly
revealed in the spectrum of Thomson scattered light.
4.6.2 Compton Scattering
One approximation implicit in our treatment of Thomson scattering is
that all the incident wave does to the electron is to cause it to
oscillate and that this oscillatory motion is added to an otherwise
unperturbed prior motion. In other words, after the scattering has
happened, the electron remains either stationary or moving at the same
velocity as it had before. [In this section we will henceforward take
the electron to be stationary prior to the scattering for simplicity.]
But this cannot really be right, even on a classical picture, because
we know that electromagnetic fields carry momentum. So if the wave is
scattered, changing its momentum, then the electron's momentum must
also be changed so as to conserve total momentum.
The classical effect can easily be calculated. By the symmetry of the
sin2 α angular distribution of scattering, the scattered
radiation has zero momentum on average. Therefore the momentum
imparted to the electron is just that of the incident radiation. We
saw in section 3.2.3 that the momentum density of
electromagnetic fields is equal to 1/c2 times the energy flux
density. The force exerted by the incident radiation on the
electron is equal to the total cross-section times the momentum
flux density, which is c times the momentum density. So this force
is
|
me |
⋅
v
|
0
|
= σsi / c = |
8π
3
|
re2 ϵ0 Ei2 |
1
c
|
. |
| (4.105) |
In this classical picture there is a radiation pressure, applying
over an area equal to the Thomson cross-section of the electron, which
steadily pushes it in the direction of the incident radiation.
Quantum mechanics teaches us, however, that electromagnetic radiation
is not smooth and infinitely divisible. Instead it takes the form of
photons whose energy is ħ ω when the angular frequency of
the radiation is ω. If the size of the photon, the quantum of
energy, is much less than the other energy scales in the problem, then
the classical limit discussed above, can apply. If the photon energy
is large, it cannot. Actually, the crucial question here is the
momentum of the photon but this can be related to energy and
compared with the rest energy of the electron (m0c2 = 511 keV) as
we shall see. The quantum picture, then, is that each individual
photon may, on encountering a free electron, bounce off in a
scattering event. When it does so, the photon's momentum is changed,
and the electron's momentum changes also so as satisfy
conservation. As a consequence, for energetic (large momentum)
photons, even an initially stationary electron recoils from a
scattering event with substantial momentum. This recoil leads to a
downshift in the energy (and hence frequency) of the scattered photon
that will depend on the direction in which it is scattered.
Figure 4.13:
Compton scattering geometry in the
scattering plane.
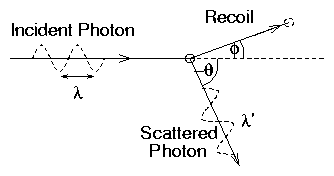
We denote the final momentum of the electron by p,
the photon energy by E before and E′ after the
scattering collision. Then the momentum of the photon is E/c
(from the energy relationship above or from our knowledge about the
relationship between energy flux and momentum of electromagnetic
fields). Then we write down the two components of momentum
conservation parallel
and perpendicular
to the incident photon, and the energy conservation:
|
E + m0c2 = E′+ |
√
|
p2c2 + (m0c2)2
|
. |
| (4.109) |
We eliminate ϕ by separating the ϕ terms in eqs
4.107 and 4.108 squaring and adding to get:
|
p2 = | ⎛
⎝
|
E
c
| ⎞
⎠
|
2
|
+ | ⎛
⎝
|
E′
c
| ⎞
⎠
|
2
|
− 2 |
EE′
c2
|
cosθ . |
| (4.110) |
And then we eliminate the momentum p by squaring the square-root
term of eq 4.109 to get
|
p2c2 = 2 m0c2(E−E′) + (E−E′)2 |
| (4.111) |
and subtracting from c2 times the previous equation to get
|
0 = EE′(1−cosθ) − m0c2(E−E′) . |
| (4.112) |
This is the equation that relates the photon energy downshift to the
angle of photon scattering. It is most often written in a form
governing the photon wavelength λ = 2πc/ω = h c /
E and using 1−cosθ = 2sin2θ/2,
|
λ′− λ = |
h
m0 c
|
2 sin2 |
θ
2
|
, |
| (4.113) |
which expresses the "Compton Shift" of wavelength in terms of the
"Compton Wavelength", λc ≡ h/m0c=2.426×10−12 m,
of the electron. A photon's wavelength equals the Compton wavelength
when its energy is equal to the rest mass of the electron,
m0c2=511 keV. Therefore the Compton shift is important only for
very energetic x-rays and for γ-rays.
The energy of the scattered photon is
and the energy lost by the photon, and hence gained as kinetic energy
by the electron is
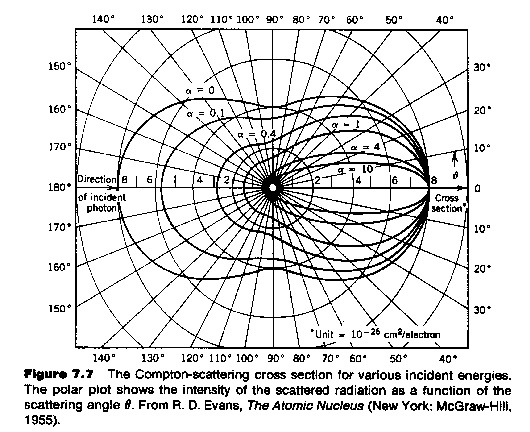
Figure 4.14:
Compton scattering
cross-section angular variation. [α ≡
E/m
ec
2].
|
|
dσ
dΩs
|
= |
re2
2
|
| ⎛
⎝
|
E′
E
| ⎞
⎠
|
2
|
| ⎛
⎝
|
E
E′
|
+ |
E′
E
|
−sin2θ | ⎞
⎠
|
. |
| (4.116) |
In this form the reduction to the Thomson cross-section at low photon
energy, so that E′/E → 1, can be
verified by integration of the Thomson formula over all possible
incident radiation polarization directions. At high photon energy,
E > mec2, forward or small angle scattering tends to
dominate the cross-section, because the (E′/E)2
term becomes small at larger angles; although for those photons that
are back-scattered θ ≈ 180o, they lose practically all
their energy to the electrons and retain only E′→ mec2/2. Figure 4.14 shows polar plots of the
cross-section at different energies.
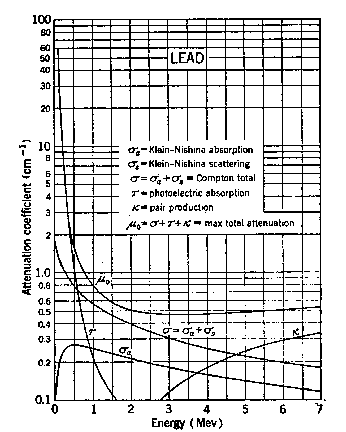
The Compton scattering process is a dominant attenuation mechanism in
the 1 to 4 MeV photon energy range. It is sometimes helpful to
distinguish between the cross-section for scattering of a photon,
given above, and the cross-section for removal of energy from a photon
beam, which is equal to the product of the scattering cross-section
and the ratio of energy loss to initial photon energy. This later is
sometimes called the Compton "absorption" cross-section since it
represents the rate at which energy is transfered from photons to
Compton scattered electrons. In either case, the attenuation of a
photon stream of intensity I is governed by a differential equation:
|
|
dI
dl
|
= − ne σI = − Z ni σI , |
| (4.117) |
where σ is the cross-section per electron, and the fact that
the Z electrons are bound to each atom is ignored since the photon
energy is so much higher than the electron binding energy. The
solutions to this equation are exponential ( ∝ exp(−neσl)) with inverse decay length neσ, which is
called the "attenuation coefficient".
Figure 4.15:
Photon attenuation
coefficients for lead. [From Evans]
|
|
Alead
ρlead Zlead
|
|
ρother Zother
Aother
|
, |
| (4.118) |
where ρ is mass density, A is atomic weight, and Z is atomic
number.