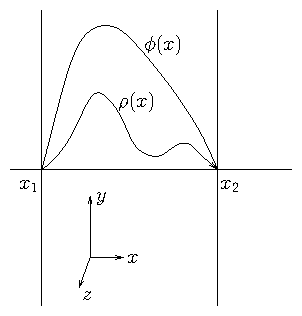HEAD PREVIOUS

Chapter 3
Two-point Boundary Conditions

Very often, the boundary conditions that determine the solution of an ordinary differential equation are applied not just at a single value of the independent variable, x, but at two points, x1 and x2. This type of problem is inherently different from the "initial value problems" discussed previously. Initial value problems are single-point boundary conditions. There must be more than one condition if the system is higher order than one, but in an initial value problem, all conditions are applied at the same place (or time). In two-point problems we have boundary conditions at more than one place (more than one value of the independent variable) and we are interested in solving for the dependent variable(s) in the interval x1 ≤ x ≤ x2 of the independent variable.

3.1  Examples of Two-Point Problems

Many examples of two-point problems arise from steady flux conservation in the presence of sources.
In electrostatics the electric potential ϕ is related to the charge density ρ through one of the Maxwell equations: a form of Poisson's equation
∇.E=−∇2ϕ = ρ/ϵ0
(3.1)
where E is the electric field and ϵ0 is the permittivity of free space.
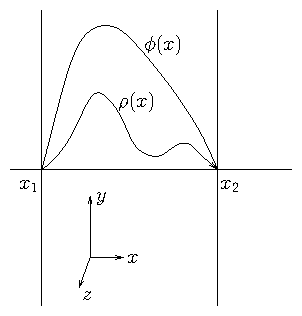
figures/slabcharge.png
Figure 3.1: Electrostatic configuration independent of y and z with conducting boundaries at x1 and x2 where ϕ = 0. This is a second-order two-point boundary problem.
In a slab geometry where ρ varies in a single direction (coordinate) x, but not in y or z, an ordinary differential equation arises
d2ϕ
dx2
 = − ρ(x)
ϵ0
 .
(3.2)
If we suppose (see Fig. 3.1) that the potential is held equal to zero at two planes, x1 and x2, by placing grounded conductors there, then its variation between them depends upon the distribution of the charge density ρ(x). Solving for ϕ(x) is a two-point problem. In effect, this is a conservation equation for electric flux, E. Its divergence is equal to the source density, which is the charge density.
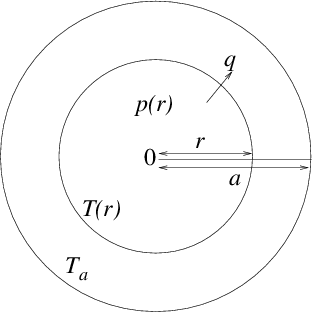
figures/cylinderheat.png
Figure 3.2: Heat balance equation in cylindrical geometry leads to a two-point problem with conditions consisting of fixed temperature at the edge, r=a and zero gradient at the center r=0.
A second-order two-point problem also arises from steady heat conduction. See Fig. 3.2. Suppose a cylindrical reactor fuel rod experiences volumetric heating from the nuclear reactions inside it with a power density p(r) (Watts per cubic meter), that varies with cylindrical radius r.
Its boundary, at r=a say, is held at a constant temperature Ta. If the thermal conductivity of the rod is κ(r), then the radial heat flux density (Watts per square meter) is
q=−κ d T
dr
 .
(3.3)
In steady state, the total heat flux across the surface at radius r (per unit rod length) must equal the total heating within it:
2πr q = −2 πr κ(r) d T
dr
 = ⌠
⌡ 		r

0 
 p(r′) 2πr′dr′.
(3.4)
Differentiating this equation we obtain:
d
dr
 ⎛
⎝ 		rκ d T
dr
⎞
⎠ 		= −r p(r).
(3.5)
This second-order differential equation requires two boundary conditions. One is T(a)=Ta, but the other is less immediately obvious. It is that the solution must be nonsingular at r=0, which requires that the derivative of T be zero there:
d T
dr
⎢
⎢

r=0 
 = 0.
(3.6)

3.2  Shooting

3.2.1  Solving two-point problems by initial-value iteration

One approach to computing the solution to two-point problems is to use the same technique used to solve initial value problems. We treat x1 as if it were the starting point of an initial value problem. We choose enough boundary conditions there to specify the entire solution. For a second-order equation such as (3.2) or (3.5), we would need to choose two conditions: y(x1)=y1, and dy/dx|x1=s, say, where y1 and s are the chosen values. Only one of these is actually the boundary condition to be applied at the initial point, x1. We'll suppose it is y1. The other, s, is an arbitrary guess at the start of our solution procedure.
Given these initial conditions, we can solve for y over the entire range x1 ≤ x ≤ x2. When we have done so for this case, we can find the value y at x2 (or its derivative if the original boundary conditions there required it). Generally, this first solution will not satisfy the actual two-point boundary condition at x2, which we'll take as y=y2. That's because our guess of s was not correct.
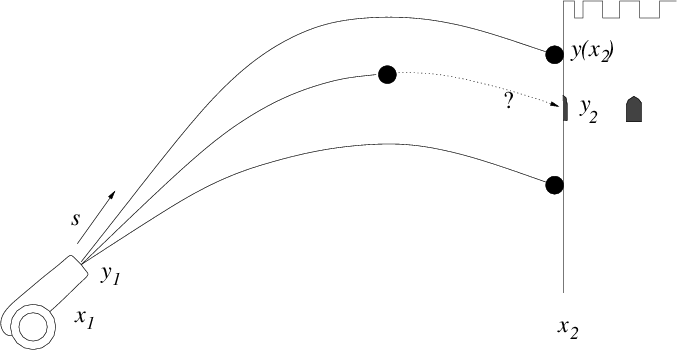
figures/cannonshoot.png
Figure 3.3: Multiple successive shots from a cannon can take advantage of observations of where the earlier ones hit, in order to iterate the aiming elevation s until they strike the target.
It's as if we are aiming at the point (x2,y2) with a cannon located at (x1,y1) (see Fig. 3.3). We elevate the cannon so that the cannonball's initial angle is dy/dx|x1=s, which is our initial guess at the best aim. We shoot. The cannonball flies over, (within our metaphor, the initial value solution is found) but is not at the correct height when it reaches x2 because our first guess at the aim was imperfect. What do we do? We see the height at which the cannonball hits, above or below the target. We adjust our aim accordingly with a new elevation s2, dy/dx|x1=s2, and shoot again. Then we iteratively refine our aim taking as many shots as necessary, and improving the aim each time, till we hit the target. This is the "shooting" method of solving a two-point problem. The cannonball's trajectory stands for the initial value integration with assumed initial condition.
One question that is left open in this description is exactly how we refine our aim. That is, how do we change the guess of the initial slope s so as to get a solution that is nearer to the correct value of y(x2)? One of the easiest and most robust ways to do this is by bisection.

3.2.2  Bisection

Suppose we have a continuous function f(s) over some interval [sl,su] (i.e. sl ≤ s ≤ su), and we wish to find a solution to f(s)=0 within that range. If f(sl) and f(su) have opposite signs, then we know that there is a solution (a "root" of the equation) somewhere between sl and su. For definiteness in our description, we'll take f(sl) ≤ 0 and f(su) ≥ 0. To get a better estimate of where f=0 is, we can bisect the interval and examine the value of f at the point s=(sl+su)/2. If f(s) < 0, then we know that a solution must be in the half interval [s,su], whereas if f(s) > 0, then a solution must be in the other interval [sl,s]. We choose whichever half-interval the solution lies in, and update one or other end of our interval to be the new s-value. In other words, we set either sl=s or su=s respectively. The new interval [sl,su] is half the length of the original, so it gives us a better estimate of where the solution value is.
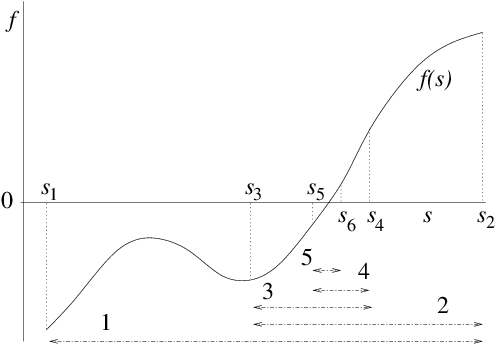
figures/bisection.png
Figure 3.4: Bisection successively divides in two an interval in which there is a root, always retaining the subinterval in which a root lies.
Now we just iterate the above procedure, as illustrated in Fig. 3.4. At each step we get an interval of half the length of the previous step, in which we know a solution lies. Eventually the interval becomes small enough that its extent can be ignored; we then know the solution accurately enough, and can stop the iteration.
The wonderful thing about bisection is that it highly efficient, because it is guaranteed to converge in "logarithmic time". If we start with an interval of length L, then at the kth interation the interval length is L/2k. So if the tolerance with which we need the s-value solution is δ (generally a small length), the number of iterations we must take before convergence is N=log2(L/δ). For example if L/δ = 106, then N=20. This is a quite modest number of iterations even for a very high degree of refinement.
There are iterative methods of root finding that converge faster than bisection for well behaved functions. One is "Newton's method", which may succinctly be stated as sk+1 = sk − f(sk)/df/ds|sk. It converges in a few steps when the starting guess is not too far from the solution. Unlike bisection, it does not require two starting points on opposite sides of the root. However, Newton's method (1) requires derivatives of the function, which makes it more complicated to code, (2) is less robust, because it takes big steps near df/ds=0, and may even step in the wrong direction and not converge at all in some cases. Bisection is guaranteed to converge after a modest number of steps. Robustness is in practice usually more important than speed.16
In the context of our shooting solution of a two-point problem, the function f is the error in the boundary value at the second point y(x2)−y2 of the inital-value solution y(x) that takes initial-value s for its derivative at x1. The bisection generally adjusts the initial-value s until |y(x2)−y2| is less than some tolerance (rather than requiring some tolerance on s).

3.3  Direct Solution

The shooting method, while sometimes useful for situations where adaptive step-length is a major benefit, is rather a back-handed way of solving two-point problems. It is very often better to solve the problem by constructing a finite difference system to represent the differential equation including its boundary conditions, and then solve that system directly.

3.3.1  Second-order finite differences

First let's consider how one ought to represent a second-order derivative as finite differences. Suppose we have a uniformly spaced grid (or mesh) of values of the independent variable xn such that xn+1−xn=∆x. The natural definition of the first derivative is
dy
dx
⎢
⎢

n+1/2 
 = ∆y
∆x
 = yn+1 − yn
xn+1 − xn
 ;
(3.7)
and this should be regarded as an estimate of the value at the midpoint xn+1/2=(xn+xn+1)/2, which we denote via a half-integral index n+1/2. The second derivative is the derivative of the derivative. Its most natural definition, therefore is
d2y
dx2
⎢
⎢

n 
 = ∆(dy/dx)
∆x
 = (dy/dx|n+1/2−dy/ dx|n−1/2)
xn+1/2−xn−1/2
 ,
(3.8)
as illustrated in Fig. 3.5.
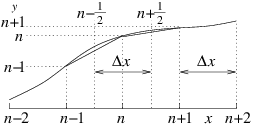
figures/2ndDerivative.png
Figure 3.5: Discrete second derivative at n is the difference between the discrete derivatives at n+1/2 and n−1/2. In a uniform mesh, it is divided by the same ∆x.
Because the first derivative is the value at n+1/2, the second derivative (the derivative of the first derivative) is the value at a point mid way between n+1/2 and n−1/2, i.e. at n. Substituting from the previous equation (3.7) we get17:
d2y
dx2
⎢
⎢

n 
 = (yn+1−yn)/∆x − (yn−yn−1)/∆x
∆x
 = yn+1 − 2 yn + yn−1
∆x2
 .
(3.9)
Now think of the entire mesh stretching from n=1 to n=N. The values yn at all the nodes can be considered to be a column vector of length N. The second derivative can then be considered to be a matrix operating on that column vector, to give the values of eq. (3.9). So, written in matrix form we have:
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
d2y/dx2|1
:
d2y/dx2|n
:
d2y/dx2|N
 ⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠ 		= 1
∆x2
 ⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
···
···
0
0
0
1
−2
1
0
0
0
···
···
···
0
0
0
1
−2
1
0
0
0
···
···
 ⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠ 		⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎝
y1
:
yn
:
yN
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎠ 		,
(3.10)
where the square N×N matrix has diagonal elements equal to −2. On the adjacent diagonals, sometimes called subdiagonals, (indices n,n+1 and n,n−1) it has 1; and everywhere else it is zero. This overall form is called tridiagonal.
If we are considering the equation
d2y
dx2
 = g(x)
(3.11)
where g(x) is some function (for example g=−ρ/ϵ0 for our electrostatic example) then the equation is represented by putting the column vector (d2y/dx2|n) equal to the column vector (gn)=(g(xn)).

3.3.2  Boundary Conditions

However, in eq. (3.10), the top left and bottom right corners of the derivative matrix have deliberately been left ambiguous, because that's where the boundary conditions come into play. Assuming they are on the boundaries, the quantities y1 and yN are determined not by the differential equation and the function g, but by the boundary values. We must adjust the first and last row of the matrix accordingly to represent those boundary conditions. A convenient way to do this when the conditions consist of specifying yL and yR at the left and right-hand ends is to write the equation as:
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
−2
0
0
0
0
0
0
1
−2
1
0
0
0
0
0
···
···
···
0
0
0
0
0
1
−2
1
0
0
0
0
0
···
···
···
0
0
0
0
0
1
−2
1
0
0
0
0
0
0
−2
 ⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠ 		⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
y1
y2
:
yn
:
yN−1
yN
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠ 		= ⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
−2yL
g2∆x2
:
gn∆x2
:
gN−1∆x2
−2yR
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠ 		.
(3.12)
Notice that the first and last rows of the matrix have been made purely diagonal, and the column vector on the right hand side (call it h) uses for the first and last rows the boundary values, and for the others the elements of g∆x2. These adjustments enforce that the first and last values of y are always the boundary values yL and yR.18
Once we have constructed this matrix form of the differential equation, which we can write:
D y = h,
(3.13)
it is obvious that we can solve it by simply inverting the matrix D and finding
y = D−1 h.
(3.14)
(Or we can use some other appropriate matrix equation solution technique.)
In general, we must make the first and last rows of the matrix equation into discrete expressions of the boundary conditions there. If instead of Dirichlet boundary conditions (value is specified), we are given Neumann conditions, that is, the derivative (e.g. dy/dx|1) is specified, a different adjustment of the corners is necessary. The most obvious thing to do is to make the first row of the matrix equation proportional to
(−1    1    0    ...) (y) = y2−y1 = ∆x(dy/dx|1).
(3.15)
However, this choice does not calculate the derivative at the right place. The expression (y2−y1)/∆x is the derivative at x3/2 rather than x1, which is the boundary19. So the scheme (3.15) is not properly centered and will give only first order accuracy.20 A better extrapolation of the derivative to the boundary is to write instead for the first row
⎛
⎝ 		− 3
2
     2    − 1
2
     0   ...⎞
⎠ 		(y) = − 1
2
 (y3−y2)+ 3
2
 (y2−y1) = ∆x(dy/dx|1).
(3.16)
This is a discrete form of the expression y′1 ≈ y′3/2−y"2.1/2∆x, which is accurate to second-order, because it cancels out the first-order error in the derivative. The same treatment applies to a Neumann condition at xN (but of course using the mirror image of the row given in eq. (3.16)).
If the boundary condition is of a more general form (the so-called Robin condition)
Ay+By′+C=0,
(3.17)
Then we want the first row to represent this equation discretely. The natural way to do this, based upon our previous forms, is to make it
⎡
⎣ 		A⎛
⎝ 		1    0    0    ...)+ B
∆x
 (− 3
2
     2    − 1
2
     0   ...⎞
⎠ 		⎤
⎦ 		(y) = −C.
(3.18)
In addition to combining the previous inhomogeneous boundary forms, this expression can also represent the specification of homogeneous boundary conditions, or in other words logarithmic gradient conditions. When C=0, the boundary condition is d(lny )/dx=y′/y=−A/B. This form (with A/B=1) is the condition that one might apply to the potential due to a spherically symmetric electrostatic charge at the outer boundary, for example.
It may be preferable in some cases to scale the first row of the matrix equation to make the diagonal entry the same as all the other diagonals, namely −2. This is done by multiplying all the row's elements of D, and the corresponding entry of h by a factor −2/D11, or −2/DNN respectively. This can improve the conditioning of the matrix, making inversion easier and more accurate.
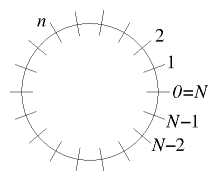
figures/periodicBC.png
Figure 3.6: Periodic boundary conditions apply when the independent variable is, for example, distance around a periodic domain.
A final type of boundary condition worth discussing is called "periodic". This expression means that the end of the x-domain is considered to be connected to its beginning. Such a situation arises, for example, if the domain is actually a circle in two-dimensional space. But it is also sometimes used to approximate an infinite domain. For periodic boundary conditions it is usually convenient to label the first and last point 0 and N. See Fig. 3.6. They are the same point; so the values at x0 and xN are the same. There are then N different points and the discretized differential equation must be satisfied at them all, with the differences wrapping round to the corresponding point across the boundary. The resulting matrix equation is then
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
−2
1
...
0
...
0
1
1
−2
1
0
0
0
0
:
···
···
···
0
0
:
0
0
1
−2
1
0
0
:
0
0
···
···
···
:
0
0
0
0
1
−2
1
1
0
...
0
...
1
−2
 ⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠ 		⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
y1
y2
:
yn
:
yN−1
yN
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠ 		= ⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
g1∆x2
g2∆x2
:
gn∆x2
:
gN−1∆x2
gN∆x2
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠ 		,
(3.19)
which maintains the pattern 1,−2,1 for every row, without exception. For the first and last rows, the subdiagonal 1 element that would be outside the matrix, is wrapped round to the other end of the row. It gives a new entry in the top right and bottom left corners.21

3.4  Conservative Differences, Finite Volumes

In our cylindrical fuel rod example, we had what one might call a "weighted derivative": something more complicated than a Laplacian. One might be tempted to write it in the following way:
d
dr
 ⎛
⎝ 		rκ d T
dr
⎞
⎠ 		= rκ d2T
dr2
 + d(rκ)
dr
 d T
dr
 ,
(3.20)
and then use the discrete forms for the first and second derivative in this expression. The problem with that approach is that first derivatives are at half-mesh-points (n+1/2 etc.), while second derivatives are at whole mesh points (n). So it is not clear how best to express this multiple term formula discretely in a consistent manner. In particular, if one adopts an asymmetric form, such as writing dT/dr|n ≈ (Tn+1− Tn)/∆x, (just ignoring the fact that this is really centered at n+1/2, not n), then the error will be of second-order in ∆x. The scheme will be accurate only to first-order. That's bad.
We must avoid that error. But even so, there are various different ways to produce schemes that are second-order accurate. Generally the best way is to recall that the differential form arose as a conservation equation. It was the conservation of energy that required the heat flux through a particular radius cylinder 2πrκdT/dr to vary with radius only so as to account for the power density at radius r. It is therefore best to develop the second-order differential in this way. First we form dT/dr in the usual discrete form at n−1/2 and n+1/2. Then we multiply those values by rκ at the same half-mesh positions n−1/2 and n+1/2. Then we take the difference of those two fluxes writing:
d
dr
 ⎛
⎝ 		rκ d T
dr
⎞
⎠
=⎛
⎝ 		rn+1/2κn+1/2 Tn+1−Tn
∆r
 − rn−1/2κn−1/2 Tn−Tn−1
∆ r
⎞
⎠ 		1
∆r
= 1
∆r2
 [                          rn+1/2κn+1/2
  Tn+1
   −(rn+1/2κn+1/2+rn−1/2κn−1/2)
  Tn
   + rn−1/2κn−1/2
  Tn−1 ].
(3.21)
The big advantage of this expression is that it exactly conserves the heat flux. This property can be seen by considering the exact heat conservation in integral form over the cell consisting of the range rn−1/2 < r < rn+1/2:
2πrn+1/2κn+1/2 dT
dr
⎢
⎢

n+1/2 
 − 2πrn−1/2κn−1/2 dT
dr
⎢
⎢

n−1/2 
 =−⌠
⌡ 		rn+1/2

rn−1/2 
 p 2πr′dr′.
(3.22)
Then adding together the versions of this equation for two adjacent positions n=k,k+1, the
dT
dr
⎢
⎢

k+1/2 

terms cancel, provided the expression for
rκ dT
dr

is the same at the same n value regardless of which adjacent cell (k or k+1) it arises from. This symmetry is present when using
dT
dr
⎢
⎢

n+1/2 
 =(Tn+1−Tn)/∆r

and the half-mesh values of rκ. The sum of the equations is therefore the exact total conservation for the region rk−1/2 < r < rk+3/2, consisting of the sum of the two adjacent cells. This process can then be extended over the whole domain, proving total heat conservation. Approaching the discrete equations in this way is sometimes called the method of "finite volumes"22. The finite volume in our illustrative case is the annular region between rn−1/2 and rn+1/2.
A less satisfactory alternative which remains second-order accurate might be to evaluate the right hand side of eq. (3.20) using double distance derivatives that are centered at the n mesh as follows
d
dr
 ⎛
⎝ 		rκ d T
dr
⎞
⎠
=⎛
⎝ 		rnκn Tn+1−2Tn+Tn−1
∆r2
 + rn+1κn+1−rn−1κn−1
2∆ r
 Tn+1−Tn−1
2∆r
⎞
⎠
= 1
∆r2
 [ (rn+1κn+1/4+rnκn−rn−1κn−1/4)
  Tn+1
−2rnκn
  Tn
+(−rn+1κn+1/4+rnκn+rn−1κn−1/4)
  Tn−1 ].
(3.23)
None of the coefficients of the Ts in this expression is the same as in eq. (3.21) unless rκ is independent of position. This is true even in the case where rκ is known only at whole mesh points so the half-point values in (3.21) are obtained by interpolation. Expression (3.23) does not exactly conserve heat flux, which is an important weakness. Expression (3.21) is usually to be preferred.

Worked Example: Formulating radial differences

Formulate a matrix scheme to solve by finite-differences the equation
d
dr
 ⎛
⎝ 		r d y
dr
⎞
⎠ 		+ rg(r)=0
(3.24)
with given g and two-point boundary conditions dy/dr=0 at r=0 and y=0 at r=N∆, on an r-grid of uniform spacing ∆.

We write down the finite difference equation at a generic position:
dy
dr
⎢
⎢

n+1/2 
 = yn+1−yn
∆
 .

Substituting this into the differential equation, we get
−rngn= d
dr
 ⎛
⎝ 		r dy
dr
⎞
⎠

n 
=
⎛
⎝ 		rn+1/2 dy
dr
⎢
⎢

n+1/2 
 − rn−1/2 dy
dr
⎢
⎢

n−1/2 
⎞
⎠ 		1
∆
=
⎛
⎝ 		rn+1/2 yn+1−yn
∆
 − rn−1/2 yn−yn−1
∆
⎞
⎠ 		1
∆
=
(rn+1/2yn+1−2rnyn+rn−1/2yn−1) 1
∆2
 .
(3.25)
It is convenient (and improves matrix conditioning) to divide this equation through by rn/∆2, so that the nth equation reads
⎛
⎝ 		rn+1/2
rn
⎞
⎠ 		yn+1−2yn+⎛
⎝ 		rn−1/2
rn
⎞
⎠ 		yn−1 = −∆2gn
(3.26)
For definiteness we will take the position of the nth grid point to be rn=n∆, so n runs from 0 to N. Then the coefficients become
rn±1/2
rn
 = n±1/2
n
 =1± 1
2n
 .
(3.27)
The boundary condition at n=N is yN=0. At n=0 we want dy/dr=0, but we need to use an expression that is centered at n=0, not n=1/2, to give second-order accuracy. Therefore following eq. (3.16) we write the equation at n=0
∆dy/dx|0=− 1
2
 (y2−y1)+ 3
2
 (y1−y0) = ⎛
⎝ 		− 3
2
     2    − 1
2
     0   ...⎞
⎠ 		(y) = 0.
(3.28)
Gathering all our equations into a matrix we have:
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
− 3
2
2
− 1
2
0
0
0
0
1− 1
2
−2
1+ 1
2
0
0
0
0
0
···
···
···
0
0
0
0
0
1− 1
2n
−2
1+ 1
2n
0
0
0
0
0
···
···
···
0
0
0
0
0
1− 1
2(N−1)
−2
1+ 1
2(N−1)
0
0
0
0
0
0
−2
 ⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠ 		⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
y0
y1
:
yn
:
yN−1
yN
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠ 		=−∆2⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
0
g1
:
gn
:
gN−1
0
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
(3.29)
 Fig. 3.7 shows the solution of an illustrative case.
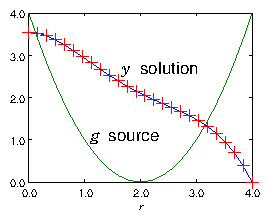
figures/cyldiff.png
Figure 3.7: Example of the result of a finite difference solution for y of eq. (3.24) using a matrix of the form of eq. (3.29). The source g is purely illustrative, and is plotted in the figure. The boundary points at the ends of the range of solution are r=0, and r=N∆ = 4. A grid size N=25 is used.

Exercise 3. Solving 2-point ODEs.

1. Write a code to solve, using matrix inversion, a 2-point ODE of the form
d2y
dx2
 = f(x)
on the x-domain [0,1], spanned by an equally spaced mesh of N nodes, with Dirichlet boundary conditions y(0)=y0, y(1)=y1.
When you have got it working, obtain your personal expressions for f(x), N, y0, and y1 from http://silas.psfc.mit.edu/22.15/giveassign3.cgi. (Or use f(x) = a + bx, a = 0.15346, b = 0.56614, N = 44, y0 = 0.53488, y1 = 0.71957.) And solve the differential equation so posed. Plot the solution.
Submit the following as your solution:
  1. Your code in a computer format that is capable of being executed.
  2. The expressions of your problem f(x), N, y0, and y1
  3. The numeric values of your solution yj.
  4. Your plot.
  5. Brief commentary ( < 300 words) on what problems you faced and how you solved them.


2. Save your code and make a copy with a new name. Edit the new code so that it solves the ODE
d2y
dx2
 + k2 y = f(x)
on the same domain and with the same boundary conditions, but with the extra parameter k2. Verify that your new code works correctly for small values of k2, yielding results close to those of the previous problem.
Investigate what happens to the solution in the vicinity of k=π.
Describe what the cause of any interesting behavior is.
Submit the following as your solution:
  1. Your code in a computer format that is capable of being executed.
  2. The expressions of your problem f(x), N, y0, and y1
  3. Brief description ( < 300 words) of the results of your investigation and your explanation.
  4. Back up the explanation with plots if you like.
HEAD NEXT