| HEAD | PREVIOUS |
Chapter 9
Energy-Resolved Diffusive Transport
When there are strong processes that drive the velocity distribution
function away from equilibrium, it is generally
important to account for the full distribution of velocities of
particles to understand their transport. Sources of particles with
kinetic energy substantially higher than the typical (e.g. thermal)
energy will have this effect. Examples include all sorts of
reactions; for example the chemical reactions
that occur in combustion, or, as we will address in this chapter, the
nuclear reactions that involve neutrons.
9.1 Collisions of Neutrons
Neutrons experience no net electric or magnetic forces, because they are uncharged, and usually gravity is ignorable; so in Boltzmann's equation the term proportional to the acceleration can usually be neglected. Self-collisions are also negligible. It is the background matter through which the neutrons are moving that provides the targets with which the neutrons collide. It can be taken to consist of practically stationary atoms. Collisions give the crucial terms in Boltzmann's equation. They arise from a whole host of different nuclear species, and the relevant cross-sections have very strong dependence on neutron kinetic energy (or equivalently speed, ). We generally sum over all the relevant species to give appropriate total source and sink rates per unit phase-space volume. In addition to the sink of neutrons, from all possible collisions, there are sources arising from scattering, and from fission reactions. For fission and scattering, as illustrated by Fig. 9.1, we consider an incoming neutron denoted with a prime (), having velocity given by speed , and direction unit vector (so ) giving rise to an outgoing (sourced) neutron with speed , and direction . The "macroscopic cross-sections" are written respectively and . They are functions of both incoming and outgoing velocity, which is denoted .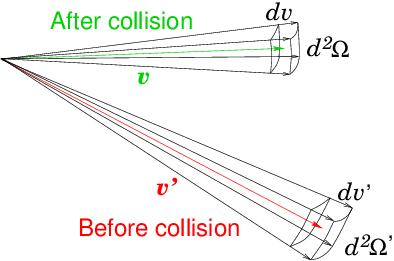
Figure 9.1: Collisions give a source of particles in as a result
of particles that (before the collision) are in
. Both induced fissions (weighted by the average
neutron yield ) and scattering events contribute. The sink
term in is the sum of all collisions that remove a
particle from .
Possible spatial dependence (on ) is implicit. Each fission
gives rise to an average number of outgoing neutrons typically
greater than one, so for source the quantity required is actually
. Also, to calculate the source we must integrate over
all possible incoming velocities, for which we write the flux
density as and the velocity element as
. Thus Boltzmann's equation becomes the
neutron transport equation:
9.2 Reduction to multigroup diffusion equations
Solving six- or seven-dimensional integro-differential equations numerically is a major undertaking. If we just simple-mindedly discretize the distribution function on finite grids in each dimension, the amount of data quickly gets out of hand. Grids of length 100 require multiple terrabytes of representation , and solving for all of the discrete elements in phase-space becomes a grand computing challenge. Although there are some reasons to tackle that challenge, it is more usual, and historically more useful, instead to reduce the dimensionality of the problem by making appropriate choices of representation. When the distribution function is nearly thermal, it is reasonable to describe it by just a few, low-order, moments of the velocity. This has the effect of reducing the three-dimensions of velocity-space to just a few dependent parameters. They are the density , the mean velocity , and the mean kinetic energy per particle, equivalent to the temperature: . Formally, taking the corresponding moments of Boltzmann's equation ends up giving us the standard fluid equations; continuity, momentum, and energy conservation. Thus, solving such a reduction has already been addressed in our discussion of numerical treatment of fluid problems. What do we do, though, when the velocity distribution is far from thermal, as it is in a reactor? We must keep account of that velocity dependence, because collision cross-sections depend upon it. A different type of approximation, useful in cases like neutron transport, because collisions are dominant, is to take the velocity anisotropy to be small. The distribution function is nearly spherically symmetric: nearly independent of ; and it is unnecessary to represent the velocity-direction dependence of in any detail.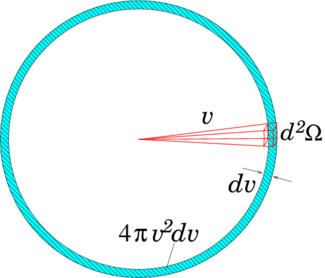
Figure 9.2: Illustrating the spherical volume in velocity-space over
which the directional integral is performed.
It is necessary to retain just enough information about the anisotropy
of to represent the directed flux density of
neutrons, which is what determines their
transport. Consider neutrons of a specific speed (i.e. in the
element at ). Integrate the full transport equation
(9.1) ( since ) over the spherical velocity space element, as illustrated in
Fig. 9.2. We will denote that
element just , to remind us of the speed choice, although its
total velocity-space-volume is . Now we denote the
distribution function integrated over direction as
Enrichment: Derivation of Diffusion Coefficient. The neutron (kinetic) transport equation (9.1) can be turned into a spatial diffusion equation by considering a fixed speed . To lowest order, we approximate the angular dependence of as being a constant plus a term proportional to ; i.e. as , where and are independent of . These are the first two terms of an expansion of the angular dependence in spherical harmonics. Reactor physics literature calls this the Approximation. Obviously this approximation only makes sense if the distribution has an approximate axis of (velocity) cylindrical symmetry, relative to which the polar angle is measured. In the absence of inherent material anisotropy, the local axis of symmetry must be in the direction of of the density gradient .
|
Integration over a spherical velocity element with
and the angle measured from the
direction . |
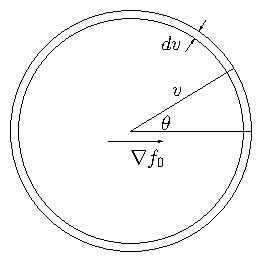
If we substitute into eq. (9.1) and equate orders of , ignoring the partial time derivative (since we presume the distribution in angle relaxes quickly), we then obtain at order
where is the part of the scattering term proportional to , which is always smaller than . (Sometimes is approximately ignorable.) Unlike scattering, fission does not contribute to this anisotropic component, except from its part in , because it is generally presumed that there is no significant correlation between the direction of neutron emission from a fission event and the incoming neutron. [The degree of anisotropy in neutrons from fission reactions is low but formally non-zero, especially at higher incoming neutron energy.] The contribution from the speed element to the directed spatial flux density (which is along the symmetry axis direction) is
Incorporating the previous equation, we then have
This is Fick's law relating a flux density to the gradient of a density , times a diffusivity
9.3 Numerical Representation of Multigroup Equations
We've made substantial progress in making the transport equation more managable, lowering its dimensionality from six phase-space dimensions to four (3 space and 1 speed). Even so, we have to choose how to represent the distribution in speed (or energy), as well as the spatial representation.9.3.1 Groups
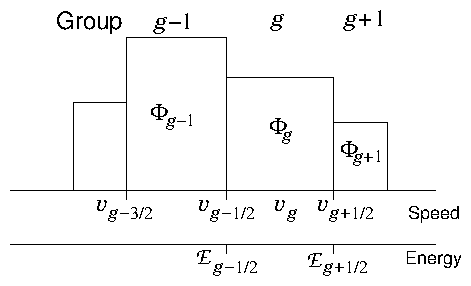
Figure 9.3: Groups are ranges in speed (equivalently energy) into which
the neutrons are lumped. They are very rarely of equal width in
speed or energy.
The natural discretization in speed is to use ranges of speed, or
equivalently energy.
In reactor physics the ranges are called "groups". It is like
representing the speed distribution as a histogram (see Fig. 9.3). A point in phase
space (particle, if you like) belongs to the (integer) group if
its speed satisfies . The
half-integer-index speeds are the extrema of the speed range belonging
to group , and this group is regarded as having a typical or
average speed . Put another way, the group can be considered to
be the integral over the finite speed element . Take there to be groups in all.
Then each neutron group separately satisfies a diffusion equation like
(9.7), except that the source integral for each
group contains, in its integral, contributions from all the other
groups, corresponding to fission neutrons appearing in one group when
they were caused by another group, or scattering directly from one
speed (group) to another.
9.3.2 Steady State Eigenvalue
The most significant aspect of the neutron diffusion equation, as applied to a fission reactor, is that it is a homogeneous equation, meaning that every term in eq. (9.9) is proportional to . That is because in a reactor essentially all the neutrons are generated by the fission reactions caused by the neutron flux itself. The steady state solution of a homogeneous equation is identically zero unless the multiplying matrix happens to be singular; in other words unless its determinant is zero. So the condition for there to be a non-trivial steady solution, representing a steadily operating reactor, to the multigroup diffusion equations is:Worked Example: Bare Homogeneous Reactor
Treat a reactor as having three neutron speed groups, whose material-interaction properties are uniform over the cuboid , , , with neutron density on the boundaries. The non-zero terms of the inverse collision length matrices (expressed in m) may be taken as:
|
Although we could construct a large finite difference block matrix and then numerically find its eigenvalue, spatially uniform material-interaction properties (collision lengths) constitute a very special case. They allow us to deduce the spatial variation of the eigenmode independently of its velocity dependence. The velocity-dependence and spatial-dependence of the eigenmodes become separable, giving rise to a distribution function of the form
Exercise 9. Neutron Transport.
1. Consider a one-group representation of neutron transport in a slab, one-dimensional, reactor of length . The reactor has uniform material properties; so that the steady diffusion equation becomes
where the diffusion coefficient (divided by velocity) , the total attenuation "macroscopic cross-section" , the scattering and fission source terms , , are simply scalar constants. is the total neutron density, because there's only one group. For convenience, write . The eigenvalue must be found for this equation. The boundary conditions at are that the neutron density satisfy
where is the outward normal at the boundary. This is essentially a non-reflective condition. It says there are no neutrons entering the reactor from outside. Formulate the finite-difference diffusion equation on a uniform mesh of nodes; node spacing . Exhibit it in the form of a matrix equation
And write out the matrix explicitly for the case (so is 55), carefully considering the incorporation of the finite-difference boundary condition. The first and last rows of that correspond to the boundary positions, are not part of the eigensolution equation. In other words, the matrix has zero first and last rows. Therefore, use the boundary conditions to eliminate and , reducing the matrix dimension by 2. Finally arrive at a 33 eigenvalue equation , where is the 33 matrix adjusted to accommodate the boundary information, and is just a scalar (equivalent to a factor times the unit matrix).
2. Implement this finite difference scheme and (using some library function) find the eigenvalue, , when , , , and or . Use large enough in your code that the solution is reasonably converged.
[Octave/Matlab hint. There are (in Octave) two routines for calculating eigenvalues: eig() and eigs(). Calling eigs(M,K) returns the largest K eigenvalues of the matrix M. Don't forget that the eigenvalue returned is solving , in other words it is the inverse of . We want just the smallest , which corresponds to the largest . We can trick this routine into giving it by using the generalized eigenvalue form , so calling eigs(eye(Nx),M,1). The eigs() routine uses an iterative technique. The eig() routine returns all the eigenvalues. It uses a direct solution technique. One then has to find the smallest, and invert it to give .]
| HEAD | NEXT |