Chapter 13
Next Steps
This book is by deliberate choice an introduction to numerical methods
for scientists and engineers that is
concise. The idea is that
brevity is the best way to grasp the big picture of computational
approaches to problem solving. However, undoubtedly for some people
the conciseness overstrains your background knowledge and
requires an uncomfortably accelerated learning curve. If so, you
may benefit by supplementing your reading with a more elementary
text
.
For readers that have survived thus far without much extra help,
congratulations! If you've really made the material your own by doing
the exercises, you have a wide-ranging essential understanding of the
application of numerical methods to physical science and engineering.
That knowledge includes some background derivations and some practical
applications, and will serve you in good stead in a professional
career. It might be all you need, but it is by no means comprehensive
The conciseness has been achieved at the expense of omitting some
topics that are without question important in certain applications. It is
the purpose of this concluding chapter to give pointers, even more
abbreviated than the preceding text, to some of these topics, and so
open the doors for students who want to go further. Of course, all of
this chapter is enrichment, and demands somewhat deeper thought in
places. If for any topic you don't "get it" on a first reading, then
don't be discouraged. References to detailed advanced textbooks are given.
13.1 Finite Element Methods
We have so far omitted two increasingly important approaches to solving
problems for complicated boundary geometries: Unstructured Meshes and
Finite Elements. Unstructured meshes enable us to accommodate in a
natural way boundaries that are virtually as complicated as we
like. The reason they are generally linked with finite element
techniques is that the finite elements approach offers a systematic
way to discretize partial differential equations on unstructured
meshes. By contrast, it is far more ambiguous how to implement
consistently finite differences on an unstructured mesh. Finite
elements are somewhat less intuitive than finite differences, and
somewhat more complex. On structured meshes they offer little
advantage to compensate; and often result in difference schemes
mathematically equivalent to finite differences. So there is far less
incentive to use finite elements on structured meshes.
The crucial difference with finite elements lies in the way the
approximation to the differential equation is formulated. We've seen
that many of the equations we need to solve in physics and engineering
are
conservation equations. They
can be expressed in differential form or in integral
form
. Most often
they are derived in integral form, and then, recognizing that the
domain over which the conservation applies is arbitrary, we conclude
that the integrand must itself be zero. That is the differential
form. The finite elements approach expresses the problem as being to
minimize the weighted integral of a finite representation of the
equation. So it is in a sense a return to integral form, but with a
specific set of weightings that we will explain in a moment.
Consider an elliptic equation of the type that arises from diffusion
and many other conservation principles:
Suppose we multiply this equation by a weight function
, and recognize that (for a differentiable
)
|
|
|
When we
integrate it over the entire solution domain volume
whose surface is
, then
using Gauss's (divergence) theorem
, we get
|
|
|
Remember that, provided
exactly satisfies the original
differential equation, this integral equation is exactly satisfied
for all possible weight functions,
. This fact is expressed by
saying that the integral is a "weak form"
of the
differential equation. However, we are going to represent
by a
functional form that has only a discrete number of
parameters. Generically
|
|
|
where
is a known function that satisfies the boundary
conditions,
is a discrete set of functions and
are the
parameters consisting of a set of coefficients to be found. This
discrete
-representation will therefore satisfy the differential
equation only approximately.
Boundary conditions on the surface
are important. To
avoid getting bogged down in discussing them, we assume that
Dirichlet (fixed
) conditions are applied. By expressing
as the sum of the part we are solving for, that satisfies
homogeneous boundary conditions
, plus some known
function
that satisfies the inhomogeneous conditions but not
the original equation, we simplify the functions
. They are
all zero on the boundary.
One benefit of the right hand side of eq. (
13.3) is that we
now have only first-order derivatives of the dependent variable
. We can therefore permit ourselves the freedom of a
-representation with discontinuous gradient without inducing the
infinities that would occur if we used the second-order form
. We still usually require
to be
everywhere continuous to avoid infinities from
. The
general approach of finite elements is to require the
residual, consisting of the right hand side of
eq. (
13.3), to be as close as possible to zero by adjusting
the parameters determining
. That optimized situation will be
the solution.
Of course, we need at least
equations to determine all the
coefficients
. These will be obtained from different choices of
the weight function
. Naturally we also represent the range of
possible weight functions discretely with a limited number of
parameters (but at least
). The most common choice of
representation is to take it to be represented by exactly the same
functions
. This choice makes sense since it allows the weight
function approximately the same freedom as
itself; it would be
unprofitable to apply far more detailed and flexible
functions
than can be represented by
. This choice, which goes by the name
Galerkin method, also gives rise to
symmetric matrices, which is often advantageous.
Substituting the total
representation of eq. (
13.4)
in the integral expression eq. (
13.3), and using for
one
after the other the functions
, we get a set of
equations
which can be written in matrix form as
where
is the column vector of coefficients
to be
determined. The
matrix
is symmetric, with coefficients
|
|
|
And the column vector
has coefficient values
|
|
|
In the mechanics field, which was where finite element
techniques mostly grew up,
is called the stiffness
matrix
,
the force vector
, and
the
displacement vector
.
This treatment has shown in principle how an integral approach can
reduce our partial differential equation to a matrix equation, to
which the various approaches to matrix inversion can be
applied to find the solution. But to be specific, we need to decide
what to use for the basis functions
. They are each defined
over the entire domain, but it will greatly reduce the number of
non-zero entries of
if we choose basis functions that are
localized, i.e. have non-zero value only in a small region of the
domain. Then when
and
refer to functions that are localized in
non-overlapping local regions, their corresponding overlap
integral
is zero. Various choices of localized basis
function
are possible, but if we think of the function as being defined at a
mesh of
nodes , then a piecewise
linear
representation arises from basis functions that are identified with
each node and vary linearly from unity at the node to zero at the
adjacent nodes. In one dimension, these are "triangle
functions"
(sometimes called "tent" functions),
whose derivatives are bipolar "box functions"
as illustrated in Fig.
13.1.
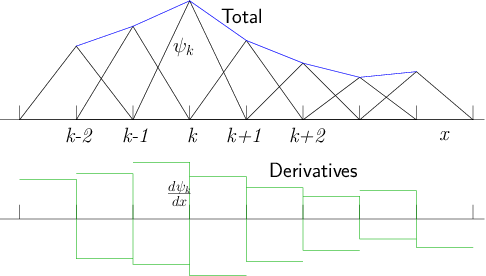
Figure 13.1: Localized triangle functions in one dimension, multiplied by
coefficients, sum to a
piecewise linear total function. Their derivatives are box functions
with positive and negative parts. They overlap only with adjacent functions.
Such a set of functions will give rise to a matrix
that is
tridiagonal
, just as was the case for finite
differences in one dimension. Using smoother, higher order, functions
representing the elements is sometimes advantageous. Cubic Hermite
functions, and cubic B-splines are two examples. They lead to a matrix
that is not quite as sparse, possessing typically seven non-zero
diagonals (in 1-dimension). Their ability to treat higher-order
differential equations efficiently compensates for the extra
computational complexity and cost.
In multiple dimensions, the geometry becomes somewhat more
complicated, but, for example, there is a straightforward extension of
the piecewise linear treatment to an unstructured mesh of
tetrahedra
in three dimensions.
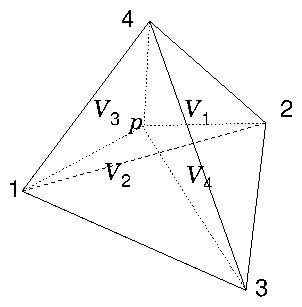
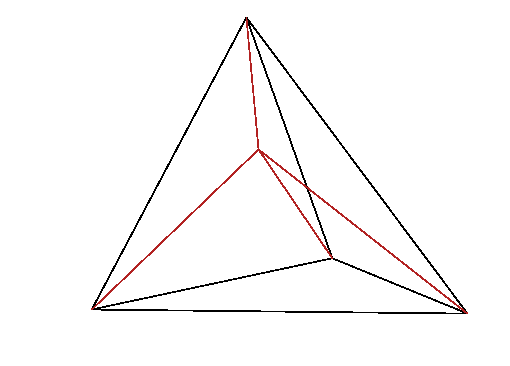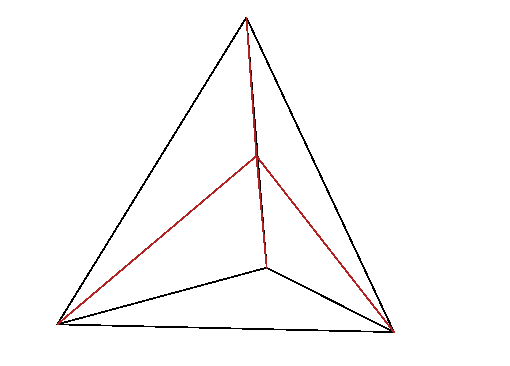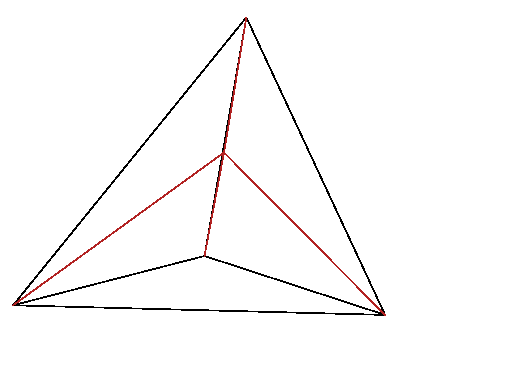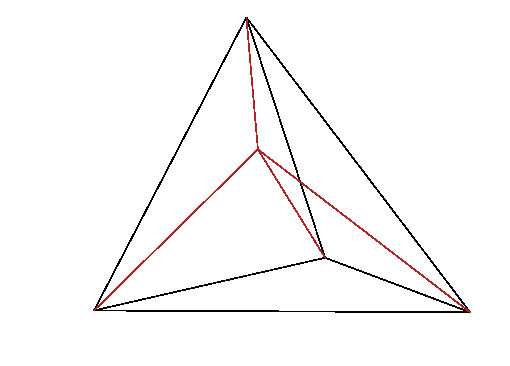
Figure 13.2: In linear interpolation within a tetrahedron, the lines from
a point
to the corner nodes of the tetrahedron, divide it into
four smaller tetrahedra, whose volumes sum to the total volume. The
interpolation weight of node
is proportional to the
corresponding volume,
.
For any point within a particular tetrahedron,
the interpolated value of the function is taken to be equal to a
weighted sum of the values at the four corner nodes. The weight of
each corner is equal to the volume of the smaller tetrahedron obtained
by replacing the corner with the point of interest, divided by the
total volume of the original tetrahedron, which Fig.
13.2 illustrates
. The
function associated with a node
is unity at
that node and decreases linearly to zero along every connection leg
to an adjacent node. The
interpolation
formula within a single
tetrahedral element is then
|
|
|
In the resulting matrix
the only non-zero overlap integrals
(coefficients) for each row
are those for nodes
that connect
to node
. The number of such connections is generally small,
amounting to typically about ten per node, but depending on
the details of the mesh. Therefore
is very sparse; and the
necessary computational effort to obtain the solution can be greatly
reduced when advanced sparse-matrix techniques are employed.
More complicated meshes are also possible, using as elements other
polyhedra
such as hexahedra (non-rectangular
cubes). Also higher order interpolations of the solution within the
elements are sometimes used. These lead to increasing complications
in handling the geometrical aspects of the problem. (Even without
these enhancements, the coding complications are already significant.)
Generally, mesh-generation libraries or applications are used to
construct the nodal mesh and its connections. Then the overlap
integrals need to be evaluated to construct the matrix
and
the vector
.
In
addition to open source libraries, many commercial computing packages
provide the mechanisms for mesh generation, integration, and equation
discretization, often with substantial graphical user interfaces to
ease the process.
13.2 Discrete Fourier Analysis and Spectral Methods
A function
, defined over a finite range of its
argument
can be expressed in terms of a Fourier series
of discrete frequencies
as.
|
|
|
where the Fourier coefficient for integer
is
|
|
|
Actually the expression (
13.9) gives a function
that is
periodic in
with period
.
Numerical representations are not usually continuous; they are
discrete. So suppose the function
is given only at uniformly
spaced argument values
for
, where
, and write
. Then these
discrete
values
of
allow
us to determine only
Fourier coefficients. It is intuitive that
these should be the
lowest (absolute) frequency components,
since one clearly cannot meaningfully represent frequencies higher than
roughly
on this discrete mesh. The lowest
frequencies
are those for which
. This observation immediately
refines the qualification of how high a frequency can be represented
on a discrete mesh. The highest frequency
has
, giving
. This limit is called the Nyquist
limit
.
If, discarding all pretence at rigor, we decide to approximate
as
a sum of Dirac delta functions
(which gives approximately correct integrals), then
the integral for
(
13.10) can be expressed
approximately
as a
sum
:
|
|
|
Now we notice that the final expression for
is
periodic
with period
; that is,
. It is therefore convenient to
consider the range of frequency index
to be re-ordered
by replacing every negative
by the positive value
. Then
runs from
to
. One should remember, though that the upper
half of this range really represents negative
frequencies. Incidentally, the periodicity of
illustrates that
one can equally well consider
to represent
any frequency
with
an integer. That is because sampling a
continuous function
at
gives values independent of
. Thus, all frequencies higher than the
Nyquist limit
, contained in a continuous signal sampled
discretely, are shifted into the Nyquist range and appear at a lower
absolute frequency in the sampled representation. This effect is called aliasing
.
The
discrete Fourier transform and its inverse can thus be
considered to be
|
|
|
Substituting for
in this expression for
, one obtains
coefficients that are sums of the form
which is zero if
and
if
. Therefore these two equations are exact, and could have been
simply adopted as definitions from the start. The discrete Fourier
transforms need not be considered
approximations to continuous
transforms; but it is helpful to recognize their relationship to
Fourier series representations of continuous functions.
Of course we aren't really interested in quantities that consist of a
set of delta functions. If, instead of simply multiplying by
, we convolve
with a triangle function
that is unity at
and descends linearly to zero at
,
then we will recover a piecewise linear function whose values at
are
. This is a much closer representation of the sort of
function we might be considering.
The Fourier transform of a
convolution of two functions is the product of their Fourier
transforms.
|
|
|
Therefore the Fourier coefficients
corresponding to
the piecewise linear form of
are the expressions in eq. (
13.12)
multiplied by the scaled Fourier transform of the triangle function, namely
|
|
|
So when dealing with continuous functions, and interpolating using the
inverse transform, eq. (
13.9), one ought probably to filter the
signal in frequency space. Multiplying by the sinc-squared function
, with
is the
equivalent of doing piecewise linear interpolation. At the highest
absolute frequency,
, where
, the filter reaches its first zero. It modestly
limits the frequency bandwidth of the signal.
It turns out to be possible to evaluate discrete Fourier transforms
(by successively dividing the domain in half) much faster than
implementing the
multiplications implied by performing
the sums in eq. (
13.12) one after the other. The
algorithms
that reduce the computational effort to of order
multiplications are called Fast Fourier Transforms
. They, naturally enough, find important uses in
spectral analysis and filtering. But, less obviously, they also
provide powerful techniques for solving partial differential
equations by representing the solution in terms of a finite number of
Fourier coeffients, as an alternative to a finite number of discrete
values.
Spectral representation is
most powerful for linear problems in which there is an ignorable
coordinate
because of some inherent
symmetry. In such situations each Fourier component becomes
independent of the others. What's more, the Fourier components are
the eigenmodes (in the direction of symmetry) of the
problem. Consequently it is sometimes the case that including a very
few such Fourier components, even as few as one, can represent the
solution. In effect, this practically lowers the dimensionality of
the problem by one, leading to major computational advantage. The
equations can be formulated in terms of Fourier modes in the symmetry
direction and finite differences in the other direction(s). For
separable
linear problems like this,
there is actually no pressing need for the Fourier Transforms to be
Fast, because the solution in space only needs to be
reconstructed after the solution in terms of Fourier modes has been
found.
If the equations to be solved are non-linear, however, or the symmetry is only
approximate, then different Fourier modes are coupled together. Then a
larger number of modes is necessary, and the computational advantage
becomes less. Even so, there are sometimes substantial remaining
benefits to a spectral representation, provided the Fourier transform
is fast. The advantages can be understood as follows.
Suppose we have a partial differential equation in which we wish to
represent the
coordinate by a Fourier expansion. The
representations of the other coordinates and their differentials do
not affect this question. Consider the equation to consist of a part
that is linear in the dependent variable
,
and a part
that is quadratic
; so
|
|
|
Here
,
,
are linear
-differential
operators, for example:
. We represent
by a sum of
Fourier modes
, where for an
-domain of length
,
. Substituting a Fourier mode into a linear operator gives rise
to an algebraic multiplier. For example
. So
, where
is the multiplier arising from
for the
mode. The equations that determine the
are found by Fourier
transforming the differential equation we started with:
|
|
|
Substituting in the Fourier expansion of
, and using the orthonormal
properties of the modes:
we get
|
|
|
The sum arising from the quadratic term couples all the individual
modal equations
together. Without it they
would be uncoupled. The coupling term has the form of a convolution
sum. To evaluate the sum directly requires for each equation
that
we evaluate on average
terms, for a total computational
multiplication count of approximately
(because there are four
multiplications per term) per solution step. Generally a nonlinear
equation must be solved by iterative steps in which the nonlinear term
must be evaluated. An alternative way to evaluate the nonlinear term
at each step is to transform back to
-space, perform the
multiplication on the
-space
, and then
fast Fourier transform (FFT)
the product
again to obtain the sum term for the Fourier mode equation
(
13.17).
The differencing to evaluate the operators
and
costs a few multiplications, say
. The product for all
values
will then cost
. And the two FFTs will be only approximately
. Therefore the total cost of this alternative scales like
. Thus, using the FFT approach reduces the
computational cost scaling to
.
Some extra questions arise concerning aliasing, but
this FFT approach is nevertheless used to good advantage for some
applications.
13.3 Sparse Matrix Iterative Krylov Solution
We stopped our development of iterative
linear system solution, which we saw in Chapter
6 is at
the heart of solving most boundary-value differential equations,
before introducing the most significant modern developments in this
field. These are associated with the name of Krylov. Here we give the
barest introduction. A modern text book should be consulted for more
details. First, as far as terminology is concerned, the name refers to
the use of the
subspace of a vector
space that is accessed by repeated multiplications by the same
matrix. The Krylov subspace
of dimension
generated by a matrix
from an initial vector
consists of all vectors that can be expressed in the form of a sum of
coefficients times the vectors
, for
. The expression
means
matrix multiply
the unit matrix
by
,
times.
The reason why this subspace is so important, is that it encompasses
all the vectors that can be accessed by an iterative scheme that uses
simply addition, scaling and multiplication by
. Multiplication by a sparse matrix involves far fewer
computations than by a full matrix, or than inversion of a sparse
matrix. Therefore iterative solution techniques that require only
sparse matrix
multiplications will be fast. Indeed the matrix itself may
never need to be formed, all that is needed is an algorithm for
multiplying by it. Let's consider how we might construct such an
interative scheme for solving
for
given
. After say
iterations, we have a
vector
which we hope is nearly the solution. The extent to
which it is not yet the solution is given by the extent to which the
residual
is non-zero. If the matrix
is not very different from the
identity matrix, then an intuitive scheme for obtaining the next
iteration vector
would be to add the residual to
and take
In
practice it is better to use an increment
chosen to be
like
, but "conjugate"
to previous
increments (in a sense to be explained), and scaled by a coefficient
chosen to minimize the resulting residual
. Thus
,
which means
|
|
|
Different schemes use different choices of
and
. The search direction
, is chosen to be
|
|
|
where
is an optional matrix, omitted (or, equivalently, the
identity) in the
simplest case. The coefficients
are chosen so as to satisfy
the conjugacy condition that we'll specify in a moment (eq.
13.23).
If we start from an initial vector
, so
(without loss of generality
), each
and
generated by the iteration, consists of sums of terms like
with
. In other words, they
are members of the Krylov subspace
. The general description "Krylov"
technique applies to all approaches that use this repeated
multiplication process.
We suppose that minimizing the residual is taken to mean minimimizing
a bilinear
form
,
where
is a fixed symmetric matrix to be chosen
later. Setting the differential of this form with respect to
equal to zero we get
|
|
|
whose solution is
|
|
|
and which gives a new residual
that is
orthogonal (in the sense of eq. (
13.21):
) to
the search direction. The conjugacy condition
on the search
directions is then taken to be that
|
|
|
which requires
(substituting from eq.
13.20)
|
|
|
The residual minimization process produces a series of residuals and
search directions having orthogonality
properties
that can be used to advantage. The first property is
Mutual
Orthogonality, which is that
|
|
|
This fact follows inductively, assuming that the condition holds up to
. Premultiplying eq. (
13.19) by
gives
|
|
|
For
the right hand side's first term is zero by hypothesis and
the second is zero by conjugacy (
13.23). For
, the left
hand side is zero by eq. (
13.21). Therefore mutual
orthogonality holds up to
and so for all
.
The second property is
Residual Orthogonality. This
follows from Mutual Orthogonality. Because
and
(
) span the same Krylov subspace,
orthogonality of a vector to all of one set implies orthogonality to
all of the other. Therefore we can replace the
in eq. (
13.25) with
and conclude
|
|
|
The final property is obtained by premultiplying eq. (
13.20) by
which
demonstrates that the non-zero scalar products with
of
and
are the same:
|
|
|
The first of these is equal to the denominator of
, in eq. (
13.22).
Residual Orthogonality enables us to demonstrate conditions on
an expression nearly the same as the numerator of
. We premultiply a version of eq. (
13.19)
using index
by
to get (for
)
|
|
|
The first term on the right hand side is zero by Residual Orthogonality. The
left hand side is also zero by Residual Orthogonality except when
.
Therefore, the combination
is zero except when
. This last form is equal to the
numerator of
provided that
| (1) | and are symmetric, |
| (2) | and commute. |
Those conditions are sufficient to ensure that only one of
the
, namely
, is non-zero. It can be rewritten
|
|
|
and
is also generally rewritten as
|
|
|
There is a major advantage to the property of having only one non-zero
coefficient, which we'll call the
"currency-property"
. It is that the
iteration requires only the
current residual and search
direction vectors, rather than all the previous vectors back to
zero. In big problems, the vectors are long. Keeping all of them
would require costly increase of storage space, and of arithmetic.
Having done the derivation for a general choice of bilinear matrix
and matrix
, we can consider various different
popular iteration schemes
as examples with different choices
of
and
.
The
Conjugate Gradient algorithm
takes
and
. The inverse of
is not required to be calculated because
(which
equals
) always appears multiplied by
. Conjugacy
is then
, and Orthogonality is
. We require
to be symmetric for the
scheme to work.
A different choice is called the
Minimum Residual
scheme,
and
, in which
is chosen
to mimimize
, with the result that Conjugacy is
and Mutual Orthogonality is
. This scheme again satisfies the
conditions for only
to be non-zero, provided that
is symmetric. It then has efficiency similar to the
Conjugate Gradient scheme.
If
is
not symmetric, then if we wish the
currency-property to hold, permitting us to retain only current
vectors, we must implement a compound scheme in which the compound
matrix
is symmetric. The best way to do this is usually
the
Bi-conjugate Gradient scheme,
in which the iteration is applied to compound vectors
,
, and
with
,
and
. Since
the commutation requirements are
immediately fulfilled. The extra costs of this scheme compared with
the Conjugate Gradient scheme are its doubled vector length
, and the
requirement to be able to multiply by
as well as by
. It is generally much more efficient than other approaches to
symmetrization, such as writing
, even when
retains sparsity properties. The Bi-conjugate
Gradient scheme has essentially the same range of eigenvalues as the
original matrix, whereas
squares the eigenvalues.
Unfortunately the same matrix symmetrization approach does not work
for the Minimum Residual scheme, because the commutation properties
are not preserved. For non-symmetric matrices one requires a
Generalized Minimum Residual (GMRES)
method
. It does not symmetrize the matrix, and does not possess the
currency-property. It therefore needs to retain
multiple older vectors to implement its conjugacy, and so requires
more storage. To limit the growth of storage, it needs to be restarted
after a moderate number of steps. The iterations are often called
after the name of their inventor, Arnoldi. So GMRES is a "restarted
Arnoldi"
method. It leads to a somewhat more
complicated but also quite robust scheme.
Solution of a set of
nonlinear differential equations over a
large domain of
mesh points is not itself just a linear system
solution. Suppose the equations for
the entire domain can be written
where
is a vector function whose
different components
represent the (e.g.) finite difference equations obeyed at all the
mesh points, and
represents the
unknowns (typically the
values at the mesh points) being solved
for. The most characteristic solution method for such a system is a
multidimensional Newton's method. We define the
Jacobian
matrix of
as the square
matrix
Then Newton's method
is a series of iterations of the form
where
is the change from one Newton step to the
next, and
evaluated at the current
position must
be used. The question is, how to solve this to find
?
Well, each Newton step now
is a linear problem, so the
techniques we've been discussing apply. For the big sparse systems we
get from differential equations, we want to apply an iterative scheme
for each solve of
. So we are dealing with a lower
level of iteration. (There are Newton iterations of iterative solves.) If an
iterative Krylov technique is used for the
solve, then
we only need to
multiply by the Jacobian matrix; we don't
actually need to form it explicitly. The multiplication of any vector
by the Jacobian in the vicinity of
can
be treated approximately as
|
|
|
where
is a suitable small parameter. Therefore, rather than
calculating and storing the big Jacobian matrix, all one requires, to
perform a multiplication of a vector by it, is to evaluate the function
at two nearby
s separated by a vector proportional
to
. This approach goes by the name
"Jacobian-free Newton
Krylov"
method.
At the beginning of this section, the idea of iterative solution was
motivated by the supposition that
is not very different from
the identity matrix so that the natural vector update is
. The speed of convergence of the iterations of any Krylov
method gets faster the closer to
the matrix is
. It is therefore usually well worth the effort to transform
the system so that
is close to identity. This process is
called
preconditioning. It consists of seeking a solution to
the modified, yet equivalent, equation
where
is easy to invert and is "similar to
" in
the sense that
well approximates the inverse of
. In point of fact, our general treatment already incorporated the
possibility of preconditioning. The matrix
serves precisely the role of
. One does not
generally multiply by
, and one may not even find
it. Instead, the preconditioning is woven into the iterative solution
by finding a preconditioned residual
, which formally equals
, but is in practice the solution of
. Therefore the combined iterative algorithm
is
| 1. | Update the residual ,
via . |
| 2. | Solve the system to
find the preconditioned residual . |
| 3. | Update the search direction using , via
. |
| 4. | Increment and repeat from 1. |
We've already encountered a preconditioner. In the Bi-conjugate
gradient scheme it was formally the compound matrix
. It makes
, which is closer to
than
is, and will be as close as
is to
. That is why the Bi-conjugate gradient scheme has the same
condition number as the original asymmetric matrix
. We might
be able to do even better than this by making the compound preconditioner
, giving
.
Here
is the additional
preconditioner chosen as an easily
inverted approximation to
.
There are many other possible preconditioners for Krylov schemes. The
preconditioning step 2 might even itself consist of some modest number
of steps of an iterative matrix solver of a different type, for
example approximate SOR inversion of
. In a sense, then,
preconditioning interleaves two different approximate matrix solvers
together, in an attempt to gain the strengths of both. In order to
preserve the currency-property and avoid retaining past residuals, we
must observe the commutation and symmetry requirements. Conjugate
gradient schemes take
and so always
commute. The only other requirements are that the preconditioning
matrix (as well as
) be symmetric so that
is symmetric (which requires that
be
symmetric). The GMRES scheme does not possess the currency-property; so
it does not have to use symmetric preconditioning.
At the very least, any Krylov system should be Jacobi
preconditioned. The Jacobi
consists of the diagonal matrix
whose elements are the diagonals of
. Jacobi preconditioning
is completely equivalent to scaling the rows of the system so that all
of the matrix diagonal entries become one. It is usually most efficient simply
to perform that scaling rather than using an explicit Jacobi
preconditioner. When all the diagonal entries are already equal, as
they are for many cases where
represents spatial finite
differences, the system is already effectively Jacobi
preconditioned. Other preconditioners generally require specific
sparse-matrix partial decomposition in order to minimize their
costs. It is hard to predict their computational advantage. Sometimes
they dramatically reduce the number of iterations, but for sparse
matrices they also generally significantly increase the arithmetic per
iteration.
13.4 Fluid Evolution Schemes
13.4.1 Incompressible fluids and pressure correction
In Chapter
7 we saw that for fluid flow speed small
compared with the sound speed
the CFL
criterion forced us to take small timesteps
. So, as the sound speed gets greater (compared with other speeds
of interest) an explicit solution of a certain time duration requires
more and more, smaller and smaller time-steps. It becomes a
stiff system, of the type discussed in section
2.3, in which a large disparity exists between the
scales of different modes. Now
increases if
becomes
large. Remember we've expressed the equation of state as
. A large value of
arises if the fluid
in question is very
incompressible. Formally, a completely
incompressible
fluid is represented by the limit
, in which the sound speed becomes infinite. For
large
, it takes a large increase in pressure to cause a small
increase in density. Solving nearly incompressible fluid equations
using an explicit approach, like the Lax-Wendroff scheme, will be
computationally costly. This is a generic problem for all types of
hyperbolic problems. It arises because of having to represent a large
range of velocity all the way from the velocities of interest up to
the speed of propagation of the fastest wave in the problem (the sound
wave in our example)
.
However, very often we actually don't care much about the propagation
of very fast sound waves. They aren't of interest, for example, in
many problems concerning the flow of
liquids
In these cases,
we don't want to have to represent the sound waves; we just want them
to go away. But if we treat the fluid equations explicitly with
tolerable sized timestep, they don't go away; instead they become
unstable. What do we do? We use a numerical scheme which treats the
sound waves
implicitly, rather than explicitly
.
The Navier Stokes
equation (
7.7) is
|
|
|
where we've gathered the advective
,
viscous
, and body forces together into
for
convenience. Linear sound waves can be derived by setting
and taking the divergence of the remainder which, invoking continuity,
becomes
. Since an
equation of state
converts
-variation
into
-variation, it becomes a simple wave equation. This
observation shows that it is
the left hand side of eq. (
13.37), the relation between
and
, that we need to make implicit in order to
stabilize sound waves. If we are advancing eq. (
13.37) by
steps
in time, then an explicit scheme could be written
|
|
|
When a fluid is essentially incompressible, the equation of state can
be considered
to be
.
If
is to satisfy the continuity equation
at time-step
, then the divergence of
eq. (
13.38) gives a Poisson equation
for
:
|
|
|
The pressure
is determined by solving this Poisson equation. Note
that the second term on the right would be zero if prior steps of the
scheme were exact. It can be considered a correction term to prevent
build up of divergence error. Once having determined
we can
then solve for
. That's an explicit scheme
.
To obtain an implicit
scheme we want to use values for
the
step in the right hand side of eq. (
13.38),
especially for
. The problem (as always in implicit schemes) is
that we don't know the new (
step) values explicitly until the
advance is completed. They are not available for simple
substitution. However, we can treat the pressure approximately
implicitly by a two step process. First we calculate an intermediate
estimate
of the new flux density by a momentum
equation update using the
old pressure gradient
(a step that's explicit in pressure) as
. Next, we calculate a
correction
to the pressure to make it mostly implicit by solving the
Poisson equation
. Then we update the
flux to our approximately implicit expression:
. A number of variations on this theme of "pressure
correction"
have been used in numerical
fluid schemes
. When treating plasmas as fluids, for example
using magnetohydrodynamics, various anisotropic
fast
and slow waves appear and several methods for eliminating unwanted
fast waves have been developed
.
13.4.2 Nonlinearities, shocks, upwind and limiter differencing
When flow velocities are in the vicinity of the sound speed, a
different sort of difficulty arises in treating compressible fluids
numerically. It is that nonlinearity becomes important and fluids can
develop abrupt changes of parameters over short length scales that are
called shocks
. The problem with the Lax-Wendroff and
similar schemes in such a context is that when encountering such
abruptly changing fluid structures they generate spurious
oscillations
. This happens because such
second-order accurate difference schemes are
dispersive. Waves of short wavelength
experience numerical phase shifts
arising from the
discrete approximations. It is these dispersive phase shifts that
cause the oscillations.
A family of methods that avoids generating spurious oscillations are
those that use
upwind
differencing. These methods are one-sided finite spatial differences,
always using the upwind side of the location in question. In other
words, if the fluid velocity is in the positive
-direction, then
the gradient of a quantity
at mesh node
is taken to be given
by
. If, however, the velocity is in the
negative direction it is taken as
. The
upwind choice has the effect of stabilizing the time evolution, which
is advantageous. They also avoid introducing spurious non-monotonic
(oscillatory) behavior. But unfortunately these schemes have rather
poor accuracy. They are only first-order in
space
, and they introduce very strong
artificial (numerical) dissipation
of
perturbations that ought physically not to be damped.
There is a nonlinear way to combine higher order accuracy with the
maintenance of monotonic behavior (hence suppressing spurious
oscillations). It is to
limit the
gradients so as to prevent oscillations occurring. Oscillations are
measured generally in the form of the
"Total Variation"
.
This quantity is equal to the
difference between the end points for a monotonic series, but is
larger if there are regions of non-monotonic behavior. A Limiter
method will avoid introducing extra oscillations if it never increases
the total variation; i.e. it is "Total Variation Diminishing"
(TVD). When these ideas are combined with a representation of the
fluid variables as being given by their average value over a cell,
together with a gradient within the cell that does not necessarily
imply continuity at the cell boundary, it is possible to define
consistently schemes that have greater fidelity in representing abrupt
fluid transitions
. Nevertheless, care must be exercised in interpreting fluid
behavior in the vicinity of regions of variation with scale length
comparable to the mesh spacing. It is always safer if possible to
ensure that the fluid variation is resolved by the mesh. If it is,
then the Lax-Wendroff scheme will give second-order accurate results.
13.4.3 Turbulence
Turbulence refers to unsteady behavior in fluids
flowing fast enough to generate flow instabilities. Direct numerical
simulation (DNS)
is the most natural way to solve a problem in which all the length
scales of the turbulence can be resolved. It consists of choosing
domain size large enough to encompass the largest scale of the
problem, while dividing it into a fine enough mesh to resolve the
smallest scale of the turbulence. The smallest scale is generally that
at which viscosity
damps out the fluid
eddies. We express the order of magnitude of gradients as
: in
terms of a length scale
. Then the nonlinear inertial term,
, is balanced
by the viscous term approximately when
is
of order unity. Here
is the velocity associated with eddies of scale
, and
is the "Reynolds number"
at scale
. It is approximately unity at the finest fluid scale of the
problem. The Reynolds number of the macroscopic flow (
) is given
approximately by substituting the typical large-scale size and flow
velocity into this definition. The critical
at
which turbulence sets in is generally somewhere between a few thousand
and a few hundred thousand, depending upon geometry. Typical situations can easily give rise
to macroscopic Reynolds numbers of
or more
. Because the ratio
of largest to smallest eddy-scale
can therefore be very
great (often estimated as
), the DNS approach eventually
becomes computationally infeasible.
Large Eddy Simulation (LES)
seeks to moderate the computational
demands through an approximation that filters out all effects smaller
than a certain length scale. Fig.
13.3 helps to explain
this process. The turbulence scale length can be expressed as a
wave-number
, in a Fourier transform of the perturbations.
The turbulence
-spectrum
is
artificially cut off at a value that is generally well below the
physical range embodied in the turbulence, i.e. below the viscous
dissipation range where
. This spatial filtering permits a
less refined mesh to represent the problem. The effects of the range
that is artificially cut off can be reintroduced in an approximate way
into the equations solved. This has most often been done in the form
of an effective eddy viscosity
added to the Navier Stokes
equations. However, fit estimates for the magnitude of the eddy
viscosity are rather uncertain
.
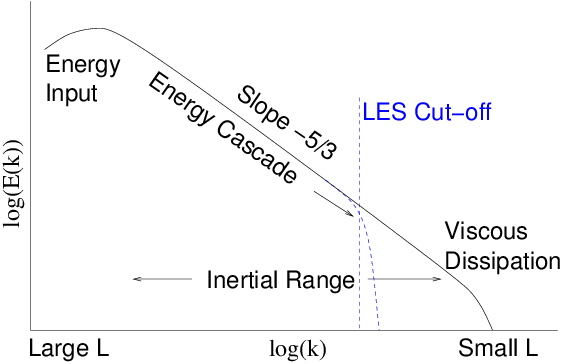
Figure 13.3: Schematic energy spectrum
of turbulence as a function
of wave number
. There is an inertial range where theory
(and experiments) indicate that a cascade of energy towards smaller
scales gives rise to a power law
. Eventually
viscosity terminates the cascade. LES artificially cuts it off at
lower
.
In fact, the finite resolution of a discrete grid representation gives
rise to an effective
cut-off in any case. If a
difference scheme is used that introduces sufficient dissipation (not
just aliasing and dispersion), it is sometimes presumed that no explicit
additional filtering is essential.
The Reynolds Averaged Navier Stokes (RANS)
is an even more
approximate treatment, which averages over all relevant time scales
leaving only the steady part of the flow. Therefore essentially
all the turbulence effects must be represented in the form of
effective transport coefficients. If we ignore for simplicity any
variation in density
, then when we time average the Navier
Stokes equation (
13.37) all the terms except
are linear. Therefore their average is
simply the average value of the corresponding quantity. The non-linear
term, though, in addition to the product of the averaged quantities,
will give rise to a contribution consisting of the average of the
square of the fluctuating part of
, i.e. the divergence of
where the over
tilde
denotes the fluctuating part and angular brackets
denote time average. The average of the fluctuating part of a quantity
is zero, but the average of the square of a fluctuation
is in general
non-zero. This extra (tensor) term
is called the
Reynolds Stress
. In order to solve the RANS
equations, one requires a way to estimate the Reynolds Stress term
from the properties of the time-averaged solution. This is done by
writing down higher-order moment equations and averaging them, which
gives rise to an equation for the evolution of the Reynolds Stress
tensor. That equation contains various other terms, including a third
order tensor of the form
. The
system of equations is "closed"
by adopting an
approximate form for the Reynolds stress evolution equation where all
the terms can be evaluated from knowledge of the flow quantities and
the Reynolds stress.
. That equation is guided by theory but with coefficients
fitted to experiments. These fits are called
"correlations"
and lead in general to a
complicated tensor evolution equation. The time-averaged Navier Stokes
equation and the Reynolds stress tensor evolution equation together
form a composite system that is then solved numerically.



